Výpočet kapacity kondenzátoru

Kapacita C je kapacita kondenzátoru přijmout (uložit a udržet) množství elektřiny Q v ampérsekundách nebo náboj Q v přívěscích. Řeknete-li tělesu, například kouli, elektrický náboj (množství elektřiny) Q, pak elektroskop zapojený mezi toto těleso a zem ukáže napětí U (obr. 1). Toto napětí je úměrné náboji a závisí také na tvaru a velikosti tělesa.

Vztah mezi nábojem Q a napětím U je vyjádřen vzorcem Q = C ∙ U.

Konstanta úměrnosti C se nazývá kapacita tělesa. Pokud má těleso tvar koule, je kapacita tělesa úměrná poloměru koule r.

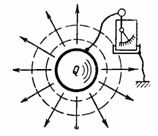
Rýže. 1.

Jednotkou měření kapacity je farad (F).

Těleso má kapacitu 1 F, když náboj 1 k vytvoří mezi ním a zemí napětí 1 V. Farady jsou velmi velkou měrnou jednotkou, proto se v praxi používají menší jednotky: mikrofarad (μF), nanofarad (nF) a pikofarad (pF)...

Tyto jednotky jsou příbuzné v následujících poměrech: 1 Ф = 10 ^ 6 μF; 1 uF = 10^6 pF; 1 nF = 10^3 pF.

Kapacita koule o poloměru 1 cm je 1,1 pF.

Akumulovat náboj může nejen izolované těleso, ale také speciální zařízení zvané kondenzátor. Kondenzátor se skládá ze dvou nebo více desek (desek), které jsou odděleny dielektrikem (izolací).

Na Obr. 2 znázorňuje obvod se stejnosměrným zdrojem připojeným ke kondenzátoru. Po zapnutí se v pravé desce kondenzátoru vytvoří kladný náboj +Q a v levé desce záporný náboj –Q. Během nabití kondenzátoru obvodem protéká proud, který se po ukončení nabíjení zastaví; pak se napětí na kondenzátoru bude rovnat e. atd. c. zdroj U. Náboj na desce kondenzátoru, napětí a kapacita souvisí poměrem Q = C ∙ U. V tomto případě se v dielektriku kondenzátoru vytvoří elektrostatické pole.

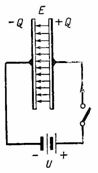
Rýže. 2.

Kapacitu kondenzátoru se vzduchovým dielektrikem lze vypočítat podle vzorce C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, kde S je plocha jedné desky, cm2; d je vzdálenost mezi deskami, cm; C je kapacita kondenzátoru, pF.

Kapacita kondenzátoru sestávajícího z n desek (obr. 3) je rovna: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

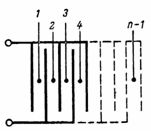
Rýže. 3.

Pokud je prostor mezi deskami vyplněn jiným dielektrikem, například papírem, kapacita kondenzátoru se zvýší o faktor ε. Při použití papírové izolace se kapacita zvýší 3krát, se slídovou izolací — 5-8krát, se sklem — 7krát atd. Hodnota ε se nazývá dielektrická konstanta dielektrika.

Obecný vzorec pro určení kapacity kondenzátoru s dielektrickou konstantou ε (epsilon) je: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Tento vzorec je užitečný pro výpočet malých proměnných kondenzátorů pro rádia.Stejný vzorec může být reprezentován jako: C = (ε_0 ∙ ε ∙ S) / d, kde ε_0 je dielektrická konstanta nebo dielektrická konstanta vakua (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε je dielektrická konstanta dielektrika.

V tomto vzorci jsou rozměry nahrazeny v metrech a kapacita je získána ve faradech.

Příklady

1. Jakou kapacitu má planeta Země, jejíž poloměr je r = 6378 km?

Protože kapacita koule o poloměru 1 cm je rovna 1,11 pF, je kapacita Země: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Kapacita koule o velikosti naší planety je relativně malá. Tuto kapacitu mají malé elektrolytické kondenzátory).

2. Určete kapacitu kondenzátoru sestávajícího ze dvou desek, z nichž každá má plochu S = 120 cm2.

Desky jsou odděleny vrstvou vzduchu o tloušťce d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Určete kapacitu kondenzátoru s údaji uvedenými v předchozím příkladu, je-li prostor mezi deskami vyplněn voskovým papírem s dielektrickou konstantou ε = 4, sklem (ε = 7), elektrokartonem (ε = 2) slída (e = 8).

Kondenzátor z voskového papíru má kapacitu C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Kapacita skleněného kondenzátoru je C = 7 ∙ 21,2 = 148,4 pF.

Kapacita kartonového kondenzátoru je C = 2 ∙ 21,2 = 42,3 pF.

Kapacita slídového kondenzátoru je C = 8 ∙ 21,2 = 169,6 pF.

4. Jakou kapacitu má vzduchový rotační kondenzátor pro rádiový přijímač skládající se z 20 desek o ploše 20 cm2, je-li vzdálenost mezi deskami 0,06 cm (obr. 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Kondenzátor znázorněný na Obr.3, sestává ze samostatných nejjednodušších kondenzátorů se dvěma deskami, jejichž počet je roven n-1.

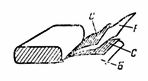
5. Papírový kondenzátor o kapacitě C = 2 μF se skládá ze dvou proužků staniolu C a dvou proužků dielektrika z voskového papíru B s dielektrickou konstantou ε = 6. Tloušťka voskového papíru je d = 0,1 mm. Ohýbané pásy jsou svinuté, přívody jsou vyrobeny z ocelových plátů. Určete délku pásu kondenzátorové oceli, je-li jeho šířka 4 cm (obr. 4).

Rýže. 4.

Nejprve určíme plochu jednoho pásu podle vzorce C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, odkud S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Délka každého pásu je l = 37680/4 = 9420 cm = 94,2 m.