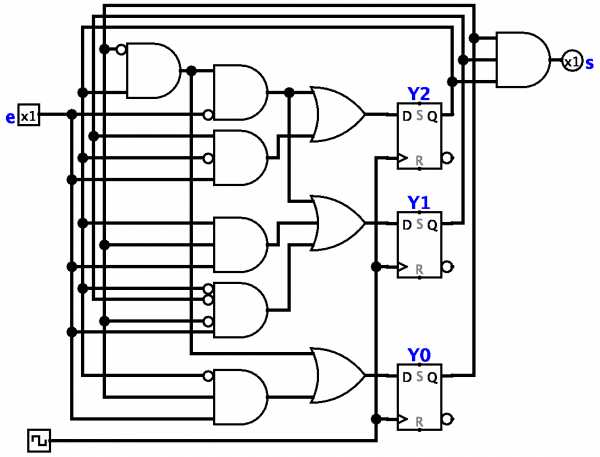
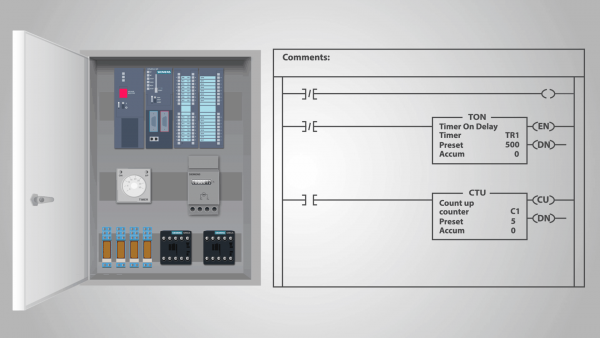
Teorie automatů, konečné automaty
Struktura, design, princip činnosti různých strojů jsou do značné míry určeny jeho funkčním účelem. Rozlišujte stroje technologické, dopravní, výpočetní, vojenské a jiné. V různých průmyslových odvětvích jsou široce zaváděny celé automatické komplexy určené k provádění složitých technologických procesů. Automaty jsou navrženy a vyrobeny tak, aby vykonávaly různé logické funkce (logické stroje).
Teorie automatů — kybernetická sekce, které vznikly pod vlivem požadavků techniky číslicových počítačů a řídicích strojů. Diskrétní automaty studované v teorii automatů jsou abstraktní modely reálných systémů (jak technických, tak biologických), které zpracovávají diskrétní (digitální) informace v diskrétních časových krocích.
Teorie automatů je založena na přesných matematických konceptech, které formalizují intuitivní představy o fungování (chování) automatu a o jeho struktuře (vnitřní struktuře).
Transformace informace je v tomto případě vždy chápána jako operace, která převádí vstupní sekvence složené z písmen vstupní abecedy na výstupní sekvence složené z písmen výstupní abecedy.
Hojně se využívá aparát matematické logiky, algebry, teorie pravděpodobnosti, kombinatoriky a teorie grafů.
Narůstal problém s teorií automatů v některých jejích částech (strukturální teorie automatů). z teorie relé-kontaktních obvodů, která se začala formovat koncem 30. let 20. století. včetně metody logické algebry.

Ve strukturní teorii automatů se studují různé typy schémat, navržených tak, aby popsaly, jak se z jednodušších komponent (prvků) správně propojených v systému vytváří složitý automat.
Další směr, zvaný abstraktní teorie automatů, studuje chování automatů (tedy povahu jimi prováděné transformace informací), přičemž abstrahuje od specifik jejich vnitřní struktury, a vznikl v 50. letech 20. století.
V rámci abstraktní teorie automatů je obsah pojmů „automat“ a „stroj“ v podstatě vyčerpán standardním popisem transformace informace, kterou automat provádí. Taková transformace může být deterministická, ale může mít také pravděpodobnostní povahu.
Nejvíce studované jsou deterministické stroje (automaty), které zahrnují konečné automaty — hlavní předmět studia v teorii automatů.
Konečný automat je charakterizován omezeným množstvím paměti (počet vnitřních stavů) a je definován pomocí přechodové funkce.S jistou rozumnou idealizací lze všechny moderní matematické stroje a dokonce i mozek z hlediska jejich fungování považovat za konečné automaty.
Pojmy „sekvenční stroj“, „Millyho automat“, „Mooreův automat“ se v literatuře (a ne jednotně všemi autory) používají jako synonyma termínu „konečný automat“ nebo pro zdůraznění určitých rysů v přechodových funkcích konečného automatu. automat.
Automat s neomezenou pamětí je Turingův stroj schopný provádět (potenciálně) jakoukoli efektivní transformaci informací. Koncept „Turingova stroje“ vznikl dříve než koncept „konečného stroje“ a je studován především v teorii algoritmů.
Teorie abstraktních automatů úzce souvisí se známými algebraickými teoriemi, například teorií pologrup. Z aplikačního hlediska jsou zajímavé výsledky charakterizující transformaci informace v automatu z hlediska velikosti paměti.
Je tomu tak např. v problémech s experimenty na automatech (práce E.F. Moorea aj.), kdy se z výsledků měření získává ta či ona informace o přechodových funkcích automatu nebo o kapacitě jeho paměti. experimenty.
Dalším úkolem je vypočítat periody výstupních sekvencí na základě dostupných informací o velikosti paměti automatu a periodách vstupních sekvencí.
Velký význam má vývoj metod pro minimalizaci paměti konečných automatů a studium jejich chování v náhodných prostředích.
V teorii abstraktních automatů je problém syntézy následující.Z hlediska nějakého jasně formalizovaného jazyka jsou podmínky napsány pro chování navrženého automatu (pro událost reprezentovanou v automatu). V tomto případě je nutné vyvinout metody, které podle každé písemné podmínky:
1) zjistit, zda existuje takový stavový automat, že jím transformované informace splňují tuto podmínku;
2) pokud ano, pak se zkonstruují přechodové funkce takového konečného automatu nebo se odhadne velikost jeho paměti.
Řešení úlohy syntézy v takové formulaci předpokládá předběžné vytvoření vhodného jazyka pro záznam provozních podmínek automatu s vhodnými algoritmy pro přechod od záznamových k tranzitivním funkcím.
Ve strukturální teorii automatů spočívá problém syntézy v konstrukci řetězce prvků daného typu, který realizuje konečný automat daný jeho přechodovými funkcemi. V tomto případě obvykle uvádějí nějaké kritérium optimality (například minimální počet prvků) a snaží se získat optimální schéma.
Jak se později ukázalo, znamená to, že některé metody a koncepty vyvinuté dříve ve vztahu k obvodům s reléovými kontakty jsou použitelné pro obvody jiného typu.
V souvislosti s rozvojem elektronických technologií jsou nejrozšířenější schémata funkčních prvků (logické sítě). Speciálním případem logických sítí jsou abstraktní neuronové sítě, jejichž prvky se nazývají neurony.
Bylo vyvinuto mnoho metod syntézy v závislosti na typu obvodů a transformaci informace, pro kterou jsou určeny (Syntéza reléových zařízení).
Dívej se -Minimalizace kombinačních obvodů, Carnotovy mapy, syntéza obvodů
Konečný automat — matematický model řídicího systému s pevnou velikostí paměti (kterou nelze za provozu zvětšit).
Koncept konečného automatu je matematická abstrakce, která charakterizuje obecné charakteristiky souboru řídicích systémů (například vícesmyčkové reléové zařízení). Všechny tyto systémy mají společné rysy, které je přirozené přijmout jako definici konečného automatu.
Každý dokončený automat má vstup vystavený vnějším vlivům a vnitřním prvkům. Pro vstupní i vnitřní prvky existuje pevný počet diskrétních stavů, které mohou nabývat.
Ke změně stavů vstupních a vnitřních prvků dochází v diskrétních okamžicích, intervaly mezi nimiž se nazývají ticks. Vnitřní stav (stav vnitřních částí) na konci pásky je určen výhradně vnitřním stavem a stavem vstupu na začátku pásky.
Všechny ostatní definice konečného automatu lze redukovat na tuto charakteristiku, zejména definice, které předpokládají, že konečný automat má výstup, který závisí na vnitřním stavu automatu v daném čase.
Z hlediska takové charakteristiky je povaha jeho vstupů a vnitřních stavů pro popis úplného automatu irelevantní. Místo vstupů a stavů se stačí podívat na jejich čísla v náhodném číslování.
Stavový automat bude nastaven, pokud je specifikována závislost jeho čísla vnitřního stavu na předchozím čísle vnitřního stavu a předchozím čísle stavu vstupu. Takový úkol může mít formu finálového stolu.
Dalším běžným způsobem, jak definovat úplný automat, je konstrukce tzv přechodové diagramy. Vstupní stavy se často nazývají jednoduše vstupy a vnitřní stavy jsou jednoduše stavy.
Konečný automat může být modelem jak technických zařízení, tak některých biologických systémů. Automaty prvního typu jsou např. reléová zařízení a různé elektronické počítače vč. programovatelné logické automaty.
V případě reléového zařízení hrají roli vstupních stavů kombinace stavů citlivých prvků reléového zařízení (každá kombinace takových stavů je «složitým stavem», charakterizovaným indikací všech citlivých prvků reléového zařízení). tyto diskrétní stavy, které mají v daném okamžiku). Podobně jako vnitřní stavy působí kombinace stavů mezilehlých prvků reléového zařízení.
Programovatelný logický kontrolér (PLC) je příkladem reléového akčního zařízení, které lze nazvat samostatným stavovým automatem.
Ve skutečnosti, jakmile je program vložen do PLC a regulátor začne počítat, není vystaven vnějším vlivům a každý následující stav je zcela určen jeho předchozím stavem. Můžeme předpokládat, že vstup má stejný stav v každém taktu.
Naopak každý konečný automat, který má jediný možný vstupní stav, se přirozeně nazývá autonomní, protože v tomto případě vnější prostředí nenese žádnou informaci, která by řídila jeho chování.
Viz také:
Využití mikroprocesorových systémů v elektrotechnice na příkladu využití PLC