Výpočet topného tělesa

Pro stanovení jednoho z hlavních parametrů drátu topného tělesa — průměru d, m (mm) se používají dva způsoby výpočtu: podle přípustného měrného plošného výkonu PF a pomocí tabulky proudových zatížení.

Přípustný měrný povrchový výkon PF= P⁄F,

kde P je výkon drátového ohřívače, W;

F = π ∙ d ∙ l — plocha ohřívače, m2; l — délka drátu, m.

Podle prvního způsobu

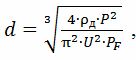
kde ρd — elektrický odpor materiálu drátu při skutečné teplotě, Ohm • m; U je napětí topného drátu, V; PF — přípustné hodnoty měrného plošného výkonu pro různé ohřívače:

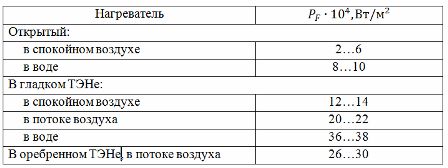
Druhá metoda využívá tabulku proudových zátěží (viz tabulka 1) sestavenou z experimentálních dat. Pro použití uvedené tabulky je nutné určit výpočtovou teplotu ohřevu Tp vztaženou ke skutečné (nebo přípustné) teplotě vodiče Td poměrem:

Tr = Km ∙ Ks ∙ Td,

kde Km je instalační faktor, který bere v úvahu zhoršení podmínek chlazení ohřívače v důsledku jeho konstrukce; Kc je faktor prostředí, uvažující zlepšení podmínek chlazení ohřívače ve srovnání se stacionárním vzduchem.

Pro topný článek z drátu stočeného do spirály Km = 0,8 … 0,9; stejné, s keramickou základnou Km = 0,6 ... 0,7; pro drát topných desek a některých topných prvků Km = 0,5 ... 0,6; pro vodič z elektrické podlahy, zeminy a topných těles Km = 0,3 ... 0,4. Menší hodnota Km odpovídá ohřívači s menším průměrem, větší hodnota většímu průměru.

Při provozu za jiných podmínek než je volná konvekce se pro topná tělesa v proudu vzduchu bere Kc = 1,3 … 2,0; pro prvky ve stojaté vodě Kc = 2,5; ve vodním toku — Kc = 3,0 … 3,5.

Pokud je nastaveno napětí Uph a výkon Pf budoucího (navrženého) ohřívače, pak jeho proud (na fázi)

Iph = Pph⁄Uph

Podle vypočtené hodnoty proudu ohřívače pro potřebnou výpočtovou teplotu jeho ohřevu dle tabulky 1 se zjistí požadovaný průměr nichromového drátu d a požadovaná délka drátu m pro výrobu ohřívače. se počítá:

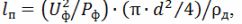
kde d je zvolený průměr drátu, m; ρd je měrný elektrický odpor vodiče při skutečné teplotě ohřevu, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

kde αр — teplotní koeficient odporu, 1/OS.

Pro určení parametrů nichromové spirály vezměte střední průměr závitů D = (6 … 10) ∙ d, stoupání spirály h = (2 … 4) ∙ d,

počet otáček

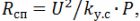
délka šroubovice lsp = h ∙ n.

Při výpočtu topných prvků je třeba mít na paměti, že odpor spirálového drátu po stlačení topného prvku

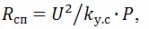
kde k (y.s) je koeficient, který zohledňuje snížení odporu spirály; podle experimentálních dat k (s) = 1,25. Je třeba také vzít v úvahu, že měrný povrchový výkon spirálového drátu je 3,5 ... 5krát větší než měrný povrchový výkon trubkového topného článku.

Při praktických výpočtech topného tělesa nejprve určete teplotu jeho povrchu Tp = To + P ∙ Rt1,

kde je teplota okolí, °C; P je výkon topného článku, W; RT1 — tepelný odpor na potrubí — rozhraní média, ОC / W.

Poté se určí teplota vinutí: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

kde Rt2 je tepelný odpor stěny potrubí, ОC / W; RT3 — tepelný odpor plniva, ОC / W; Rp1 = 1⁄ (α ∙ F), kde α je součinitel prostupu tepla, W / (m ^ 2 • ОС); F - plocha ohřívače, m2; Rt2 = δ⁄ (λ ∙ F), kde δ je tloušťka stěny, m; λ — tepelná vodivost stěny, W / (m • ОС).

Více informací o zařízení topných těles naleznete zde: Topná tělesa. Zařízení, výběr, obsluha, připojení topných těles

Tabulka 1. Tabulka proudových zátěží

Příklad 1. Vypočítejte elektrický ohřívač ve tvaru drátěné spirály podle přípustného měrného plošného výkonu PF.

Stav.Výkon ohřívače P = 3,5 kW; napájecí napětí U = 220 V; materiál drátu — nichrom Х20Н80 (slitina 20 % chrómu a 80 % niklu), proto měrný elektrický odpor drátu ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; teplotní koeficient odporu αр = 16 ∙ 10 ^ (- 6) 1 /ОС; spirála je otevřená, v kovové formě, pracovní teplota spirály je Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W / m2. Určete d, lp, D, h, n, lp.

Odpovědět. Odpor cívky: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 ohmů.

Měrný elektrický odpor při Tsp = 400 OS

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.

Najděte průměr drátu:

Z výrazu R = (ρ ∙ l) ⁄S dostaneme l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), odkud je délka drátu

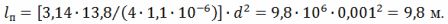
Střední průměr spirálového závitu je D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Rozteč spirály h = 3 ∙ d = 3 ∙ 1 = 3 mm.

Počet závitů spirály

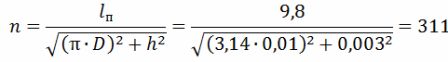
Délka šroubovice je ​​lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Příklad 2. Strukturálně vypočítejte odporový ohřívač drátu při určování průměru drátu d pomocí tabulky proudového zatížení (viz tabulka 1).

Stav. Výkon ohřívače drátu P = 3146 W; napájecí napětí U = 220 V; materiál drátu — nichrom Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; ap = 16 ∙ 10 ^ (- 6) 1 / ℃; otevřená šroubovice umístěná v proudu vzduchu (Km = 0,85, Kc = 2,0); přípustná provozní teplota vodiče Td = 470 ОС.

Určete průměr d a délku drátu lp.

Odpovědět.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

Návrhový proud ohřívače I = P⁄U = 3146⁄220 = 14,3 A.

Podle tabulky proudového zatížení (viz tabulka 1) při Tр = 800 ОС a I = 14,3 A zjistíme průměr a průřez drátu d = 1,0 mm a S = 0,785 mm2.

Délka drátu lp = (R ∙ S) ⁄ρ800,

kde R = U^ 2⁄P = 220 ^ 2⁄3146 = 15,3 Ohm, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) 10 ^ (- 6) Ohm • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

V případě potřeby lze, podobně jako v prvním příkladu, definovat D, h, n, lsp.

Příklad 3. Určete dovolené napětí trubkového elektrického ohřívače (TEN).

Stav... Cívka topného tělesa je vyrobena z nichromového drátu o průměru d = 0,28 mm a délce l = 4,7 m. Topné těleso je v klidném vzduchu o teplotě 20 °C. Charakteristiky nichromu: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. Délka aktivní části pouzdra topného tělesa je La = 40 cm.

Topné těleso je hladké, vnější průměr dob = 16 mm. Součinitel prostupu tepla α = 40 W / (m ^ 2 ∙ ° C). Tepelné odpory: výplň RT3 = 0,3 ОС / W, stěny pouzdra Rт2 = 0,002 ОС / W.

Určete, jaké maximální napětí lze použít na topné těleso, aby teplota jeho cívky Tsp nepřesáhla 1000 ℃.

Odpovědět. Teplota topného tělesa topného tělesa

Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

kde je teplota okolního vzduchu; P je výkon topného článku, W; RT1 — kontaktní tepelný odpor rozhraní potrubí-médium.

Výkon topného tělesa P = U ^ 2⁄R,

kde R je odpor topné spirály.Proto můžeme psát Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), odkud je napětí na topném článku

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Najděte R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

kde ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20)] = 1,12 ∙^ — 6) Ohm • m.

Potom R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 Ohm.

Kontaktní tepelný odpor RT1 = 1⁄ (α ∙ F),

kde F je plocha aktivní části pláště topného článku; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Najděte Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.

Určete napětí topného článku U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.

Pokud je jmenovité napětí uvedené na topném článku 220 V, pak přepětí při Tsp = 1000 OS bude 5,6 % ∙ Un.