Pokles napětí

Pojmy a vzorce

Na každém odporu r se při průchodu proudu I objeví napětí U = I ∙ r, které se obvykle nazývá úbytek napětí tohoto odporu.

Je-li v obvodu pouze jeden odpor r, připadá celé napětí zdroje Ust na tento odpor.

Pokud má obvod dva odpory r1 a r2 zapojené do série, pak součet napětí v odporech U1 = I ∙ r1 a U2 = I ∙ r2, tzn. úbytek napětí je roven napětí zdroje: Ust = U1 + U2.

Napájecí napětí se rovná součtu úbytků napětí v obvodu (2. Kirchhoffův zákon).

Příklady

1. K jakému úbytku napětí dojde na vláknu žárovky s odporem r = 15 Ohm při průchodu proudu I = 0,3 A (obr. 1)?

Rýže. 1.

Počet poklesů napětí Ohmův zákon: U = I ∙ r = 0,3 ∙ 15 = 4,5 V.

Napětí mezi body 1 a 2 svítilny (viz schéma) je 4,5 V. Lampa svítí normálně, pokud jí protéká jmenovitý proud nebo pokud je mezi body 1 a 2 jmenovité napětí (uveden je jmenovitý proud a napětí na lampě).

2. Dvě stejné žárovky pro napětí 2,5 V a proud 0,3 A jsou zapojeny do série a připojeny ke kapesní baterii o napětí 4,5 V. Jaký úbytek napětí vzniká na svorkách jednotlivých žárovek (obr. 2 ))?

Rýže. 2.

Stejné žárovky mají stejný odpor r. Když jsou zapojeny do série, protéká jimi stejný proud I. Z toho plyne, že budou mít stejné úbytky napětí, součet těchto napětí se musí rovnat napětí zdroje U = 4,5 V. Každá žárovka má napětí 4 , 5:2 = 2,25 V.

Můžete vyřešit tento problém a sekvenční výpočet. Odpor žárovky vypočítáme podle údajů: rl = 2,5 / 0,3 = 8,33 Ohm.

Proud obvodu I = U / (2rl) = 4,5 / 16,66 = 0,27 A.

Úbytek napětí na žárovce U = Irl = 0,27 ∙ 8,33 = 2,25 V.

3. Napětí mezi kolejnicí a trolejí tramvajové trati je 500 V. Pro osvětlení jsou použity čtyři stejné svítilny zapojené do série. Pro jaké napětí by měla být vybrána každá lampa (obr. 3)?

Rýže. 3.

Identické žárovky mají stejné odpory, kterými protéká stejný proud. Úbytek napětí na lampách bude také stejný. To znamená, že pro každou lampu bude 500: 4 = 125 V.

4. Dvě svítilny o výkonu 40 a 60 W o jmenovitém napětí 220 V jsou zapojeny do série a jsou zapojeny do sítě o napětí 220 V. Jaký úbytek napětí na každé z nich nastává (obr. 4)?

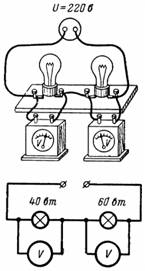
Rýže. 4.

První lampa má odpor r1 = 1210 Ohm a druhá r2 = 806,6 Ohm (ve zahřátém stavu). Proud procházející lampami je I = U / (r1 + r2) = 220 / 2016,6 = 0,109 A.

Pokles napětí v první lampě U1 = I ∙ r1 = 0,109 ∙ 1210 = 132 V.

Pokles napětí ve druhé lampě U2 = I ∙ r2 = 0,109 ∙ 806,6 = 88 V.

Žárovka s vyšším odporem má větší úbytek napětí a naopak. Vlákna obou žárovek jsou velmi slabá, ale 40W žárovka je o něco silnější než 60W žárovka.

5. Aby se napětí elektromotoru D (obr. 5) rovnalo 220 V, musí být napětí na začátku dlouhého vedení (u elektrocentrály) větší než 220 V v hodnotě pokles napětí (ztráta) online. Čím větší je odpor vedení a proud v něm, tím větší je úbytek napětí podél vedení.

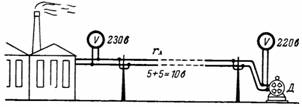Rýže. 5.

V našem příkladu je úbytek napětí v každém vodiči vedení 5 V. Pak by se napětí na přípojnicích elektrárny mělo rovnat 230 V.

6. Spotřebič je napájen baterií 80 V s proudem 30 A. Pro normální provoz spotřebiče je přípustný 3% úbytek napětí na hliníkových vodičích o průřezu 16 mm2. Jaká je maximální vzdálenost od baterie k uživateli?

Přípustný úbytek napětí ve vedení U = 3/100 ∙ 80 = 2,4 V.

Odpor vodičů je omezen přípustným úbytkem napětí rpr = U / I = 2,4 / 30 = 0,08 Ohm.

Pomocí vzorce pro stanovení odporu vypočítáme délku vodičů: r = ρ ∙ l / S, odkud l = (r ∙ S) / ρ = (0,08 ∙ 16) / 0,029 = 44,1 m.

Pokud je uživatel 22 m od baterie, bude v ní napětí menší než 80 V při 3 %, tzn. rovná 77,6 V.

7. Telegrafní vedení o délce 20 km je vyrobeno z ocelového drátu o průměru 3,5 mm. Zpětné vedení je nahrazeno uzemněním přes kovové přípojnice. Odpor přechodu mezi sběrnicí a zemí je rz = 50 Ohm.Jaké by mělo být napětí baterie na začátku vedení, když odpor relé na konci vedení je рп = 300 Ohm a proud relé je I = 5 mA?

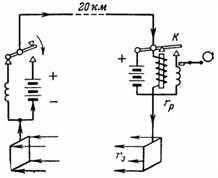
Rýže. 6.

Schéma zapojení je na Obr. 6. Při stisknutí telegrafního spínače v místě vysílání signálu přitáhne relé v přijímacím bodě na konci vedení kotvu K, která svým kontaktem zase zapne cívku záznamníku. Výstupní napětí musí kompenzovat úbytek napětí ve vedení, přijímacím relé a přechodové odpory zemnících přípojnic: U = I ∙ rl + I ∙ rр + I ∙ 2 ∙ rр; U = I ∙ (rр + рр + 2 ∙ rр).

Zdrojové napětí se rovná součinu proudu a celkového odporu obvodu.

Průřez vodiče S = (π ∙ d ^ 2) / 4 = (π ∙ 3,5 ^ 2) / 4 = 9,6 mm2.

Odpor vedení rl = ρ ∙ l / S = 0,11 ∙ 20 000 / 9,6 = 229,2 ohmů.

Výsledný odpor r = 229,2 + 300 + 2 ∙ 50 = 629,2 Ohm.

Výstupní napětí U = I ∙ r = 0,005 ∙ 629,2 = 3,146 V; U≈3,2 V.

Úbytek napětí ve vedení při průchodu proudu I = 0,005 A bude: Ul = I ∙ rl = 0,005 ∙ 229,2 = 1,146 V.

Relativně nízkého úbytku napětí ve vedení je dosaženo díky nízké hodnotě proudu (5 mA). Proto v místě příjmu musí být citlivé relé (zesilovač), které se sepne slabým 5mA impulsem a přes jeho kontakt sepne další, výkonnější relé.

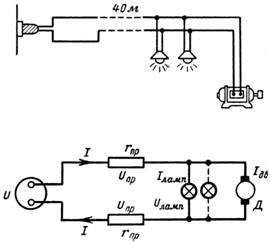
8. Jak vysoké je napětí žárovek v obvodu na Obr. 28, když: a) motor není zapnutý; b) motor se spustí; c) motor běží.

Motor a 20 svítilen je připojeno na síť 110 V. Lampy jsou určeny pro 110 V a 40 W. Startovací proud motoru je Ip = 50 A a jeho jmenovitý proud je In = 30 A.

Zavedený měděný drát má průřez 16 mm2 a délku 40 m.

Obr. 7 a podmínkách problému, je vidět, že proud motoru a lampy způsobuje pokles síťového napětí, proto bude napětí zátěže nižší než 110V.

Rýže. 7.

U = 2 ∙ Ul + Ulamp.

Proto je napětí na lampách Ulamp = U-2 ∙ Ul.

Je nutné určit úbytek napětí ve vedení při různých proudech: Ul = I ∙ rl.

Odolnost celého vedení

2 ∙ rl = ρ ∙ (2 ∙ l) / S = 0,0178 ∙ (2 ∙ 40) / 16 = 0,089 Ohm.

Proud procházející všemi lampami

20 ∙ žárovka = 20 ∙ 40/110 = 7,27 A.

Pokles napětí sítě, když svítí pouze lampy (žádný motor),

2 ∙ Ul = žárovka ∙ 2 ∙ rl = 7,27 ∙ 0,089 = 0,65 V.

Napětí v lampách je v tomto případě:

Ulamp = U-2 ∙ Ul = 110-0,65 = 109,35 V.

Při nastartování motoru budou lampy svítit tlumeněji, protože pokles napětí ve vedení je větší:

2 ∙ Ul = (žárovka + Idv) ∙ 2 ∙ rl = (7,27 + 50) ∙ 0,089 = 57,27 ∙ 0,089 = 5,1 V.

Minimální napětí žárovek při startování motoru bude:

Ulamp = Uc-2, Ul = 110-5,1 = 104,9 V.

Když motor běží, pokles napětí ve vedení je menší než při spuštění motoru, ale větší než když je motor vypnutý:

2 ∙ Ul = (žárovka + Inom) ∙ 2 ∙ rl = (7,27 + 30) ∙ 0,089 = 37,27 ∙ 0,089 = 3,32 V.

Napětí žárovek při normálním provozu motoru je:

Ulamp = 110-3,32 = 106,68 V.

I mírný pokles napětí lamp vzhledem k nominálnímu výrazně ovlivňuje jas osvětlení.