Elektrony se chovají jako vlny

Fyzici již dlouho vědí, že světlo je elektromagnetické vlnění. Dodnes o této pozici nikdo nepochybuje, protože světlo jasně demonstruje všechny znaky vlnového chování: světelné vlny se mohou navzájem překrývat, generovat interferenční obrazec, jsou také schopny se oddělit, ohýbat se kolem překážek po dobu difrakce.

Když vidíme ptáka, který chodí jako kachna, plave jako kachna a kváká jako kachna, nazýváme toho ptáka kachnou. Světlo tedy je elektromagnetická vlnana základě objektivně pozorovaných známek chování takové vlny ve světle.

Nicméně na konci 19. a 20. století měli fyzici začít mluvit o „dualismu částic a vln“ světla. Ukazuje se, že poznání, že světlo je elektromagnetické vlnění, není vše, co věda o světle ví. Vědci objevili ve světle velmi zajímavou vlastnost.

Ukazuje se, že světlo se nějak projevuje JAKO chování proudu částic.Bylo zjištěno, že energie nesená světlem se po určitém časovém úseku speciálním detektorem ukáže jako složená z jednotlivých (celých) kusů.

Proto se stalo pravdou, že energie světla je diskrétní, protože je složena jakoby z jednotlivých částic – „kvant“, tedy z nejmenších celých porcí energie. Taková částice světla, nesoucí jednotku (nebo kvantum) energie, se začala nazývat foton.

Energii jednoho fotonu zjistíme podle následujícího vzorce:

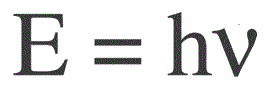
E — fotonová energie, h — Planckova konstanta, v — frekvence.

Německý fyzik Max Planck nejprve experimentálně stanovil fakt diskrétnosti světelné vlny a vypočítal hodnotu konstanty h, která se objevuje ve vzorci pro zjištění energie jednotlivých fotonů. Tato hodnota se ukázala jako: 6,626 * 10-34 J * s. Planck publikoval výsledky své práce v pozdních 1900s.

Vezměme si například fialový paprsek. Frekvence takového světla (f nebo v) je 7,5 * 1014 Hz Planckova konstanta (h) je 6,626 * 10-34 J * s. To znamená, že energie fotonu (E), charakteristická pro fialovou barvu, je 5 * 10-19 J. To je tak malá část energie, že je velmi obtížné ji zachytit.

Představte si horskou říčku — teče jako jeden celek a pouhým okem nelze vidět, že se říčka ve skutečnosti skládá z jednotlivých molekul vody. Dnes však víme, že makroskopický objekt — tok — je ve skutečnosti diskrétní, to znamená, že se skládá z jednotlivých molekul.

To znamená, že pokud umíme vedle proudu umístit počítadlo molekul, abychom spočítali molekuly vody procházející kolem proudícího proudu, detektor bude vždy počítat pouze celá čísla molekul vody, nikoli dílčí.

Podobně graf celkové energie fotonu E, vypočítaný v čase t — se vždy ukáže jako ne lineární (žlutý obrázek), ale stupňovitý (zelený obrázek):

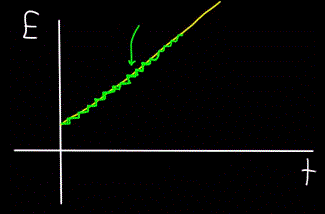
Fotony se tedy pohybují, nesou energii, proto mají hybnost. Ale foton nemá žádnou hmotnost. Jak potom můžete najít impuls?

Ve skutečnosti je pro objekty pohybující se rychlostí blízkou rychlosti světla klasický vzorec p = mv jednoduše nepoužitelný. Abychom pochopili, jak najít hybnost v tomto neobvyklém případě, pojďme se obrátit na speciální teorii relativity:

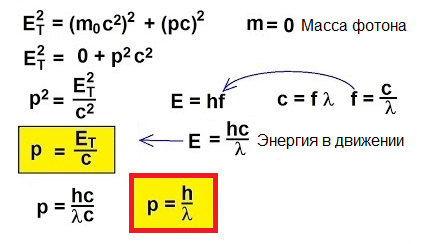
V roce 1905 Albert Einstein vysvětlil z tohoto hlediska fotoelektrický efekt… Víme, že kovová deska má v sobě elektrony, které jsou v ní přitahovány kladně nabitými jádry atomů, a proto jsou zadržovány v kovu. Pokud ale na takovou desku posvítíte světlem URČITÉ frekvence, pak můžete elektrony z desky vyrazit.

Jako by se světlo chovalo jako proud částic s hybností.A i když foton nemá žádnou hmotnost, přesto nějak interaguje s elektronem v kovu a za určitých podmínek je foton schopen elektron vyřadit.

Takže pokud má foton dopadající na desku dostatek energie, pak bude elektron vyražen z kovu a bude se pohybovat z desky rychlostí v. Takový vyřazený elektron se nazývá fotoelektron.

Protože vyřazený elektron má známou hmotnost m, bude mít určitou kinetickou energii mv.

Energie fotonu se při působení na kov přeměňuje na energii výstupu elektronu z kovu (pracovní funkce) a na kinetickou energii elektronu, kterou se vyřazený elektron začne pohybovat. z kovu, nechat to.

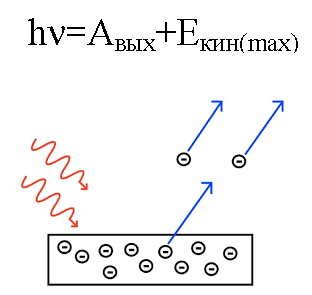
Předpokládejme, že foton o známé vlnové délce dopadá na povrch kovu, u kterého je známa pracovní funkce (elektronu z kovu). V tomto případě lze snadno zjistit kinetickou energii elektronu emitovaného z daného kovu a také jeho rychlost.

Pokud energie fotonu nestačí k tomu, aby elektron vykonal pracovní funkci, tak elektron prostě nemůže opustit povrch daného kovu a fotoelektron nevznikne.

V roce 1924 francouzský fyzik Louis de Broglie předložit průlomovou myšlenku, podle níž nejen fotony světla, ale samotné elektrony se mohou chovat jako vlny. Vědec dokonce odvodil vzorec pro hypotetickou vlnovou délku elektronu. Tyto vlny byly následně nazývány „de Broglieho vlny“.

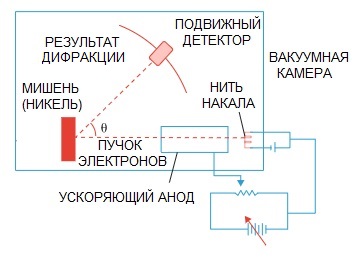
De Broglieho hypotéza byla později potvrzena. Fyzikální experiment elektronové difrakce, který provedli v roce 1927 američtí vědci Clinton Davison a Lester Germer, konečně poukázal na vlnovou povahu elektronu.

Když byl paprsek elektronů nasměrován speciální atomovou strukturou, zdá se, že detektor měl zaznamenat obraz jako částice letící jedna za druhou, což by se logicky očekávalo, kdyby elektrony byly částicemi.

Ale v praxi máme obraz charakteristický pro vlnovou difrakci. Navíc délky těchto vln jsou zcela v souladu s konceptem navrženým de Brogliem.

V konečném důsledku umožnila de Broglieho myšlenka vysvětlit princip Bohrova atomového modelu a později umožnila Erwinu Schrödingerovi tyto myšlenky zobecnit a položit základy moderní kvantové fyziky.