Výpočty magnetických obvodů

U elektrických strojů a přístrojů je magnetický tok F soustředěn v magnetickém obvodu (feromagnetické jádro) a vzduchových mezerách tohoto magnetického obvodu. Tato dráha magnetického toku se nazývá magnetický obvod.

Magnetický obvod je jako elektrický obvod. Magnetický tok Ф připomíná elektrický proud I, indukce В hustotu proudu, magnetizační síla (ns) Fн (H ∙ l = I ∙ ω) odpovídá e. atd. s

V nejjednodušším případě má magnetický obvod všude stejný průřez a je vyroben z homogenního magnetického materiálu. K určení n. s l ∙ ω potřebnou k zajištění požadované indukce B se odpovídající intenzita H určí z magnetizační křivky a vynásobí se střední délkou siločáry magnetického pole l: H ∙ l = I ∙ ω = Fm.

Odtud se určí potřebný proud I nebo počet závitů ω cívky.

Složitý magnetický obvod má obvykle sekce s různými sekcemi a magnetickými materiály. Tyto sekce jsou obvykle zapojeny do série, proto každou z nich prochází stejný magnetický tok F.Indukce B v každém úseku závisí na průřezu úseku a vypočítá se pro každý úsek zvlášť podle vzorce B = Φ∶S.

Pro různé hodnoty indukce se intenzita H určí z magnetizační křivky a vynásobí se průměrnou délkou silového vedení odpovídajícího úseku obvodu. Sečtením jednotlivých prací dostaneme úplné n. c. magnetický obvod:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … která určuje magnetizační proud nebo počet závitů cívky.

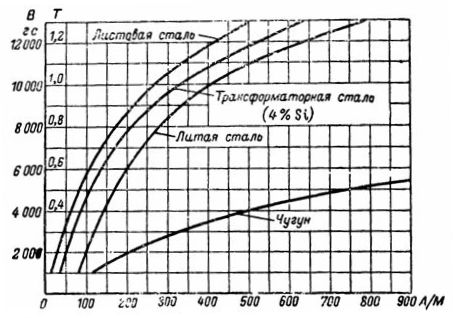
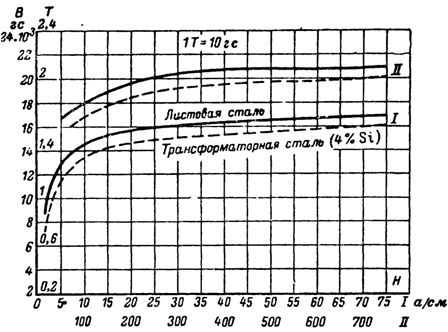
Magnetizační křivky

Příklady

1. Jaký musí být magnetizační proud I cívky o 200 závitech, aby n. c. vytvořil v litinovém prstenci magnetický tok Ф = 15700 Ms = 0,000157 Wb? Průměrný poloměr litinového prstence je r = 5 cm a průměr jeho řezu je d = 2 cm (obr. 1).

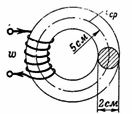
Rýže. 1.

Řez magnetického obvodu S = (π ∙ d ^ 2) / 4 = 3,14 cm2.

Indukce v jádře je: B = Φ∶S = 15700∶3,14 = 5000 G.

V systému MKSA je indukce: B = 0,000157 Wb: 0,0000314 m2 = 0,5 T.

Z magnetizační křivky litiny zjistíme požadovanou pevnost H rovnou 750 A / m pro B = 5000 G = 0,5 T. Magnetizační síla je rovna: I ∙ ω = H ∙ l = 235,5 Av.

Proto požadovaný proud I = (H ∙ l) / ω = 235,5 / 200 = 1,17 A.

2. Uzavřený magnetický obvod (obr. 2) je vyroben z ocelových plátů transformátoru. Kolik závitů musí být v cívce s proudem 0,5 A, aby se v jádře vytvořil magnetický tok Ф = 160000 Ms = 0,0016 Wb?

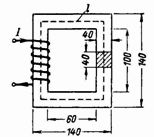
Rýže. 2.

Průřez jádra S = 4 ∙ 4 = 16 cm2 = 0,0016 m2.

Indukce jádra B = F / S = 160000/16 = 10000 Gs = 1 T.

Podle magnetizační křivky transformátorové oceli zjistíme pro B = 10 000 Gs = 1 T intenzitu H = 3,25 A / cm = 325 A / m.

Průměrná délka siločáry magnetického pole je l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0,48 m.

Magnetizační síla Fm = I ∙ ω = H ∙ l = 3,25 ∙ 48 = 315 ∙ 0,48 = 156 Prům.

Při proudu 0,5 A je počet závitů ω = 156 / 0,5 = 312.

3. Magnetický obvod znázorněný na Obr. 3 je podobný magnetickému obvodu z předchozího příkladu, až na to, že má vzduchovou mezeru δ = 5 mm. Co by mělo být. s. a proud cívky tak, aby magnetický tok byl stejný jako v předchozím příkladu, tj. F = 160000 Ms = 0,0016 Wb?

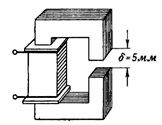
Rýže. 3.

Magnetický obvod má dva sériově zapojené úseky, jejichž průřez je stejný jako v předchozím příkladu, tedy S = 16 cm2. Indukčnost je také rovna B = 10000 G = 1 T.

Průměrná délka ocelové magnetické čáry je o něco kratší: lс = 48-0,5 = 47,5 cm ≈0,48 m.

Magnetické napětí v této sekci magnetického obvodu je Hc ∙ lc = 3,25 ∙ 48≈156 Av.

Síla pole ve vzduchové mezeře je: Hδ = 0,8 ∙ B = 0,8 ∙ 10000 = 8000 A / cm.

Magnetické napětí v průřezu vzduchové mezery Hδ ∙ δ = 8000 ∙ 0,5 = 4000 Av.

Vyplňte n. c. je rovna součtu magnetických napětí v jednotlivých úsecích: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. I = (I ∙ ω) / ω = 4156/312 = 13,3 A.

Jestliže v předchozím příkladu byl požadovaný magnetický tok zajištěn proudem 0,5 A, pak pro magnetický obvod se vzduchovou mezerou 0,5 cm je k získání stejného magnetického toku zapotřebí proud 13 A. Z toho je patrné, že vzduchová mezera, i když v poměru k délce magnetického obvodu nepatrná, značně zvyšuje potřebné n. v. a proud cívky.

4. Magnetický tok transformátoru je vypočítán na F = 72000 Ms. Je vyžadován výpočet n.s.a magnetizační proud primárního vinutí o 800 závitech. V jádru transformátoru je mezera δ = 0,2 mm. Rozměry jádra transformátoru jsou uvedeny na Obr. 4. Průřez jádra S = 2 ∙ 3 ​​​​​​= 6 cm2 (transformátory s jádry tohoto tvaru se nazývají pancéřované).

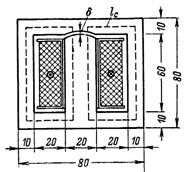
Rýže. 4.

Indukce jádra a vzduchové mezery B = F / S = 72000/6 = 12000 G.

Podle magnetizační křivky transformátorové oceli pro B = 12000 G určíme intenzitu: Hc = 5 A / cm.

Průměrná délka magnetické čáry v oceli je lс = 2 ∙ (6 + 3) = 18 cm.

Napětí ve vzduchové mezeře Hδ = 0,8 ∙ B = 9600 A / cm.

Magnetizační síla I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0,02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0,35 A.

V pancéřovém jádru se magnetický tok rozdělí na dvě části, které jsou uzavřeny podél bočních tyčí, jejichž průřez je S / 2 a průměrná délka magnetické čáry je lc. V důsledku toho je magnetický obvod zcela analogický magnetickému obvodu běžného transformátoru se společným jádrem S a délkou elektrického vedení lc.

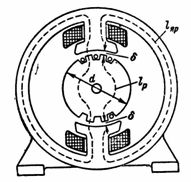
5. Magnetický tok stejnosměrného stroje F = 1280000 Mks. Magnetický obvod obsahuje ocelolitinové jho s průměrnou délkou magnetického vedení lа = 80 cm, rotor sestavený z elektroocelových desek s průměrnou délkou pole lр = 18 cm a dvě vzduchové mezery δ 0,2 cm každá. = 8 ∙ 20 cm2; průřez rotoru a pólu Sр = 12 ∙ 20 cm2... Vypočítejte n. p. a počet závitů pólové cívky, je-li v ní maximální magnetizační (budící) proud 1 A (obr. 5).

Rýže. 5.

Indukce v třmenu a pólu Bя = Ф / Sя = 1280000/160 = 8000 G.

Napětí na jho a pólu podle magnetizační křivky ocelolitiny při Bя = 8000 G se rovná:

H = 2,8 A/cm.

Magnetizační síla v řezu třmenu HЯ ∙ la = 2,8 ∙ 80 = 224 Av.

Indukce v rotoru, pólu a vzduchové mezeře Br = Ф / Ср = 1280000/240 = 5333 G.

Napětí v rotoru vyrobeném z ocelových plátů při Br = 5333 Gs Hrp = 0,9 A / cm,

a magnetické napětí sekce rotoru Hр ∙ lр = 0,9 ∙ 18 = 16,2 Av.

Napětí ve vzduchové mezeře Hδ = 0,8 ∙ Bδ = 0,8 ∙ 5333 = 4266,4 A / cm.

Magnetické napětí v průřezu vzduchové mezery Hδ ∙ 2 ∙ δ = 4266,4 ∙ 2 ∙ 0,2 = 1706,56 A.

Vyplňte n. c. rovna součtu magnetických napětí v jednotlivých úsecích: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; I ∙ ω = 224 + 16,2 + 1706,56 = 1946,76 Prům.

Počet závitů ve dvou pólových cívkách ω = (I ∙ ω) / I = 1946,76 / 1≈2000.