Linearizace charakteristik snímačů

Linearizace charakteristik snímače — nelineární transformace výstupní hodnoty snímače nebo jí úměrné veličiny (analogové nebo digitální), která dosahuje lineárního vztahu mezi naměřenou hodnotou a hodnotou, která ji představuje.

Pomocí linearizace lze dosáhnout linearity na stupnici sekundárního zařízení, ke kterému je připojen snímač s nelineární charakteristikou (např. termočlánek, tepelný odpor, analyzátor plynů, průtokoměr atd.). Linearizace charakteristik snímače umožňuje získat potřebnou přesnost měření prostřednictvím sekundárních zařízení s digitálním výstupem. To je nutné v některých případech při připojování snímačů k záznamovým zařízením nebo při provádění matematických operací s měřenou hodnotou (např. integrace).

Z hlediska charakteristiky kodéru působí linearizace jako inverzní funkční transformace.Pokud je charakteristika snímače reprezentována jako y = F (a + bx), kde x je naměřená hodnota, a a b jsou konstanty, pak by charakteristika linearizéru zapojeného do série se snímačem (obr. 1) měla vypadat takto: z = kF (y), kde F je inverzní funkce F.

Výsledkem je, že výstup linearizátoru bude z = kF(F(a + bx)) = a' + b'x, tj. lineární funkce naměřené hodnoty.

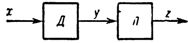
Rýže. 1. Blokové schéma zobecněné linearizace: D — snímač, L — linearizátor.

Dále se škálováním závislost z redukuje na tvar z '= mx, kde m je vhodný faktor měřítka. Pokud je linearizace provedena kompenzačním způsobem, tj. na základě servosystému, jako je obr. 2, pak by charakteristika převodníku linearizační funkce měla být podobná charakteristice snímače z = cF (a + bx), protože linearizovaná hodnota naměřené hodnoty je převzata ze vstupu převodníku funkčního linearizéru a jeho výstup je porovnán s výstupní hodnotou snímače.

Charakteristickým znakem linearizátorů jako funkčních převodníků je relativně úzká třída jimi reprodukovaných závislostí omezená na monotónní funkce, která je dána typem charakteristiky snímače.

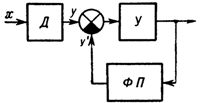
Rýže. 2. Blokové schéma linearizace založené na sledovacím systému: D — snímač, U — zesilovač (převodník), FP — funkční převodník.

Linearizátory lze klasifikovat podle následujících kritérií:

1. Podle způsobu nastavení funkce: prostorová ve formě šablon, matic apod., ve formě kombinace nelineárních prvků, ve formě digitálního výpočetního algoritmu, zařízení.

2.Podle stupně flexibility schématu: univerzální (tj. rekonfigurovatelné) a specializované.

3. Podle povahy strukturálního diagramu: otevřený (obr. 1) a kompenzační (obr. 2) typ.

4. Ve formě vstupních a výstupních hodnot: analogové, digitální, smíšené (analogově-digitální a digitálně-analogové).

5. Podle typu prvků použitých v obvodu: mechanické, elektromechanické, magnetické, elektronické atd.

Linearizátory prostorových funkcí zahrnují především vačkové mechanismy, vzory a nelineární potenciometry. Používají se v případech, kdy je naměřená hodnota každého převodního stupně prezentována ve formě mechanického pohybu (vačky — pro linearizaci charakteristik manometrických a transformátorových snímačů, modely — v zapisovacích, nelineárních potenciometrech — v potenciálových a můstkových obvodech ).

Nelinearita charakteristik potenciometru je dosažena navíjením na profilované rámy a dělením metodou po částech lineární aproximací manévrováním sekcí s vhodnými odpory.

U linearizátoru založeného na elektromechanickém servosystému potenciometrického typu s nelineárním potenciometrem (obr. 3) se linearizovaná hodnota jeví jako úhel natočení nebo mechanické posunutí. Tyto linearizéry jsou jednoduché, všestranné a široce používané v centralizovaných řídicích systémech.

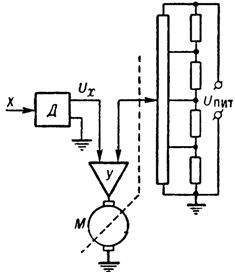
Rýže. 3. Linearizátor pro elektromechanický servosystém potenciometrického typu: D — snímač s výstupem ve formě stejnosměrného napětí, Y — zesilovač, M — elektromotor.

Nelinearity charakteristik jednotlivých prvků (elektronické, magnetické, tepelné atd.) se využívají v parametrických funkčních převodnících. Mezi funkčními závislostmi, které vyvíjejí, a charakteristikami senzorů však obvykle není možné dosáhnout úplné shody.

Algoritmický způsob nastavení funkce se používá u digitálních převodníků funkcí. Jejich předností je vysoká přesnost a stabilita charakteristik. Využívají matematické vlastnosti jednotlivých funkčních závislostí nebo princip lineární aproximace po částech. Například parabola je vyvinuta na základě vlastností druhých mocnin celých čísel.

Například digitální linearizér je založen na metodě po částech lineární aproximace, která funguje na principu plnění přibližujících se segmentů pulzy s různou opakovací frekvencí. Frekvence plnění se skokově mění na hraničních bodech blížících se segmentů podle programu vloženého do zařízení podle typu nelinearity. Linearizovaná veličina se pak převede na jednotný kód.

Částečnou lineární aproximaci nelinearity lze také provést pomocí digitálního lineárního interpolátoru. V tomto případě zůstávají frekvence plnění interpolačních intervalů konstantní pouze v průměru.

Výhody digitálních linearizérů založených na metodě lineární aproximace dílů jsou: snadná rekonfigurace akumulované nelinearity a rychlost přepínání z jedné nelinearity na druhou, což je důležité zejména u vysokorychlostních centralizovaných řídicích systémů.

Ve složitých řídicích systémech obsahujících univerzální kalkulátory, stroje lze linearizaci provádět přímo z těchto strojů, ve kterých je funkce zabudována ve formě odpovídajícího podprogramu.