RMS hodnoty proudu a napětí

Střídavý sinusový proud má různé okamžité hodnoty během období. Je přirozené položit si otázku, jaká hodnota proudu bude měřena ampérmetrem zařazeným do obvodu?

Při výpočtu obvodů střídavého proudu, stejně jako elektrických měření, je nepohodlné používat okamžité nebo amplitudové hodnoty proudů a napětí a jejich průměrné hodnoty za určité období jsou nulové. Navíc elektrický účinek periodicky se měnícího proudu (množství uvolněného tepla, dokonalý chod atd.) nelze odhadnout pomocí amplitudy tohoto proudu.

Nejpohodlnější bylo zavedení pojmů tzv. efektivních hodnot proudu a napětí... Tyto pojmy jsou založeny na tepelném (neboli mechanickém) působení proudu, které nezávisí na jeho směru.

Odmocnina hodnota střídavého proudu - jedná se o hodnotu stejnosměrného proudu, při které se během periody střídavého proudu uvolňuje ve vodiči stejné množství tepla jako při střídavém proudu.

K vyhodnocení přijatých opatření střídavý proud, porovnáme jeho působení s tepelným účinkem stejnosměrného proudu.

Stejnosměrný výkon P A procházející odporem r bude P = P2r.

Střídavý výkon je vyjádřen jako průměrný vliv okamžitého výkonu Az2r za celou dobu nebo průměr (I am x sinωT)2 NS r za stejnou dobu.

Nechť je průměrná hodnota t2 za periodu M. Zrovnáme-li výkon stejnosměrného proudu a výkonu střídavého proudu, máme: Az2r = Mr -n, odkud Az = √M,

Veličina I se nazývá efektivní hodnota střídavého proudu.

Průměrná hodnota i2 při střídavém proudu se stanoví následovně.

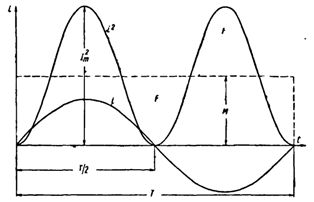
Sestrojme sinusovou proudovou křivku. Umocněním každé okamžité hodnoty proudu získáme křivku P versus čas.

AC efektivní hodnota

Obě poloviny této křivky leží nad vodorovnou osou, protože záporné proudy (-i) ve druhé polovině periody při druhé mocnině dávají kladné hodnoty.

Sestrojte obdélník se základnou T a plochou rovnou ploše ohraničené křivkou i2 a vodorovnou osou. Výška obdélníku M bude odpovídat průměrné hodnotě P za období. Tato hodnota periody, vypočtená pomocí vyšší matematiky, bude rovna 1/2 I2m... Proto M. = 1/2 I2m

Protože efektivní hodnota střídavého proudu Im je Im = √M, pak nakonec I = Im / √2

Podobně vztah mezi efektivními hodnotami a hodnotami amplitudy pro napětí U a E má tvar:

U = Um / √2E = Em / √2

Efektivní hodnoty proměnných jsou označeny velkými písmeny bez indexů (I, U, E).

Na základě výše uvedeného můžeme říci, že efektivní hodnota střídavého proudu je rovna takovému stejnosměrnému proudu, který při průchodu stejným odporem jako střídavý proud uvolňuje současně stejné množství energie.

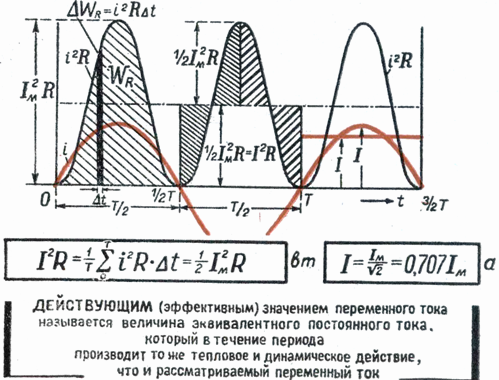
Elektrické měřicí přístroje (ampérmetry, voltmetry) zahrnuté v obvodu střídavého proudu udávají efektivní hodnoty proudu nebo napětí.

Při konstrukci vektorových diagramů je vhodnější odložit nikoli amplitudu, ale efektivní hodnoty vektorů. Za tímto účelem se délky vektorů jednou zkrátí o √2. Tím se nezmění umístění vektorů na diagramu.