Impulsní proud

V různých elektronických zařízeních, například v elektronických a polovodičových zařízeních, t. abych neopakoval úvahy dvakrát, budeme mluvit pouze o proudech, ale vše, co s proudy souvisí, platí i pro napětí.

Pulzující proudy, které mají konstantní směr, ale mění svou hodnotu, mohou být různé. Někdy se aktuální hodnota změní z nejvyšší na nejnižší nenulovou hodnotu. V ostatních případech se proud sníží na nulu. Li obvod stejnosměrného proudu se při určité frekvenci přeruší, pak po určité časové intervaly není v obvodu žádný proud.

Na Obr. 1 ukazuje grafy různých vlnových proudů. Na Obr. 1, a, b, změna proudů nastává podle sinusová křivka, ale tyto proudy by neměly být považovány za sinusové střídavé proudy, protože směr (znaménko) proudu se nemění. Na Obr.1, c znázorňuje proud sestávající ze samostatných pulzů, to znamená krátkodobých "výbojů" proudu, oddělených od sebe pauzami delšího nebo kratšího trvání, a často se nazývá pulzní proud. Různé pulzní proudy se od sebe liší tvarem a dobou trvání pulzů a také rychlostí opakování.

Je vhodné považovat pulsující proud jakéhokoli druhu za součet dvou proudů – stejnosměrného a střídavého, nazývaného termické nebo složkové proudy. Jakýkoli pulzující proud má stejnosměrné a střídavé složky. To se mnohým zdá divné. Ve skutečnosti je koneckonců pulzující proud proud, který teče stále jedním směrem a mění svou hodnotu.

Jak poznáte, že obsahuje střídavý proud, který mění směr? Procházejí-li však dva proudy — stejnosměrný a střídavý — současně stejným vodičem, ukáže se, že v tomto vodiči poteče pulzující proud (obr. 2). V tomto případě by amplituda střídavého proudu neměla překročit hodnotu stejnosměrného proudu. Stejnosměrný a střídavý proud nemohou protékat vodičem odděleně. Přidávají se k obecnému toku elektronů, který má všechny vlastnosti pulsujícího proudu.

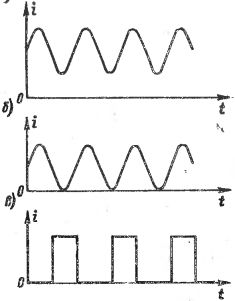
Rýže. 1. Grafy různých vlnových proudů

Součet střídavých a stejnosměrných proudů lze znázornit graficky. Na Obr. 2 ukazuje grafy stejnosměrného proudu rovného 15 mA a střídavého proudu s amplitudou 10 mA. Pokud sečteme hodnoty těchto proudů pro jednotlivé body v čase, vezmeme-li v úvahu směry (znaménka) proudů, dostaneme graf vlnových proudů znázorněný na obr. 2 s tučnou čarou. Tento proud se pohybuje od nízké hodnoty 5 mA do vysoké hodnoty 25 mA.

Uvažovaný součet proudů potvrzuje platnost zobrazení pulzujícího proudu jako součtu stejnosměrných a střídavých proudů. Správnost tohoto znázornění potvrzuje i fakt, že pomocí některých zařízení je možné složky tohoto proudu od sebe oddělit.

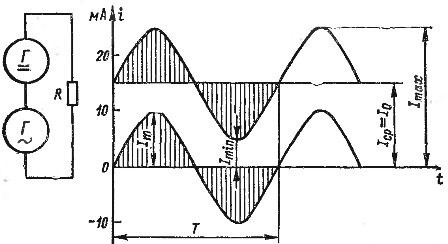
Rýže. 2. Získání pulzujícího proudu přidáním stejnosměrného a střídavého proudu.

Je třeba zdůraznit, že jakýkoli proud může být vždy reprezentován jako součet několika proudů. Například proud 5 A lze považovat za součet proudů 2 a 3 A tekoucích jedním směrem nebo součet proudů 8 a 3 A tekoucích různými směry, tedy jinými slovy za rozdíl mezi proudy 8 a 3 A. Není těžké najít jiné kombinace dvou nebo více proudů dávajících dohromady 5 A.

Zde je naprostá podobnost s principem sčítání a rozkladu sil. Působí-li na jakýkoli předmět dvě stejně směrované síly, lze je nahradit jednou společnou silou. Síly působící v opačných směrech lze nahradit jednotkovým rozdílem. Naopak danou sílu lze vždy považovat za součet odpovídajících stejně směrovaných sil nebo za rozdíl mezi opačně směrovanými silami.

Stejnosměrné nebo sinusové střídavé proudy není nutné rozkládat na složkové proudy. Nahradíme-li pulsující proud součtem stejnosměrných a střídavých proudů, pak aplikací známých zákonů stejnosměrných a střídavých proudů na tyto složky proudů je možné vyřešit mnoho problémů a provést potřebné výpočty související s pulsujícím proudem.

Koncepce pulzujícího proudu jako součtu stejnosměrných a střídavých proudů je konvenční.Samozřejmě nelze předpokládat, že v určitých časových intervalech stejnosměrný a střídavý proud k sobě po drátě skutečně teče. Ve skutečnosti neexistují dva opačné toky elektronů.

Ve skutečnosti je pulzující proud jediný proud, který v průběhu času mění svou hodnotu. Správnější je říci, že pulzující napětí nebo pulzující EMF lze reprezentovat jako součet konstantní a proměnné složky.

Například na OBR. 2 ukazuje, jak algebraicky je konstantní emf jednoho generátoru přidána k proměnné emf jiného generátoru. V důsledku toho máme pulzující EMF, který způsobuje odpovídající pulzující proud. Podmíněně však lze uvažovat, že konstantní EMF vytváří v obvodu stejnosměrný proud a střídavý EMF - střídavý proud, který po sečtení tvoří pulzující proud.

Každý pulzující proud lze charakterizovat maximálními a minimálními hodnotami Itax a Itin, jakož i jeho konstantními a proměnnými složkami. Konstantní složka se značí I0. Je-li střídavou složkou sinusový proud, pak se jeho amplituda značí It (všechny tyto veličiny jsou znázorněny na obr. 2).

Nemělo by se zaměňovat s It a Itaxem. Také maximální hodnota proudové vlny Imax by neměla být nazývána amplitudou. Termín amplituda obvykle označuje pouze střídavé proudy. Ohledně pulzujícího proudu lze hovořit pouze o amplitudě jeho proměnné složky.

Konstantní složku pulzujícího proudu lze nazvat jeho průměrnou hodnotou Iav, tedy aritmetickým průměrem. Pokud skutečně vezmeme v úvahu změny v jedné periodě pulzujícího proudu znázorněného na obr.2 je jasně vidět následující: v první polovině cyklu se k proudu 15 mA přičte řada hodnot změnou složky proudu, v rozmezí od 0 do 10 mA a zpět na 0, a ve druhé polovině -cyklu, přesně stejné hodnoty proudu se odečítají od proudu 15 mA.

Proto je proud 15 mA skutečně průměrná hodnota. Protože proud je přenos elektrických nábojů průřezem vodiče, pak Iav je hodnota takového stejnosměrného proudu, který za jednu periodu (nebo za celý počet period) přenese stejné množství elektřiny jako tento pulzující proud. .

Pro sinusový střídavý proud je hodnota Iav za periodu nulová, protože množství elektřiny prošlé průřezem vodiče v jedné půlperiodě se rovná množství elektřiny procházející v opačném směru během další půlperiody. Na grafech proudů znázorňujících závislost proudu i na čase t je množství elektřiny přenášené proudem vyjádřeno plochou obrazce ohraničeného proudovou křivkou, protože množství elektřiny je určeno produkt, který to.

Pro sinusový proud jsou oblasti kladných a záporných polovičních vln stejné. 2, během první poloviny periody se množství elektřiny přenášené střídavou složkou přičte k množství elektřiny přenášené proudem Iav (stínovaná oblast na obrázku). A během druhé poloviny cyklu se odebere přesně stejné množství elektřiny. V důsledku toho se po celou dobu přenáší stejné množství elektřiny jako u jediného stejnosměrného proudu Iav, to znamená, že plocha obdélníku Iav T se rovná ploše ohraničené křivkou vlnového proudu.

Konstantní složka neboli průměrná hodnota proudu je tedy určena přenosem elektrických nábojů průřezem drátu.

Současná rovnice znázorněná na Obr. 2 by měl být samozřejmě napsán v následujícím tvaru:

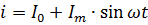
Výkon pulzujícího proudu se musí vypočítat jako součet výkonů jeho dílčích proudů. Pokud například proud zobrazený na Obr. 2, prochází rezistorem odporu R, pak je jeho výkon

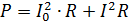
kde I = 0,7 Im je efektivní hodnota proměnné složky.

Můžete zavést koncept efektivní hodnoty vlnového proudu Id. Výkon se počítá obvyklým způsobem:

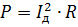
Když tento výraz přirovnáme k předchozímu a zmenšíme jej pomocí R, dostaneme:

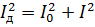
Stejné vztahy lze získat pro napětí.