Elektron v elektrickém poli

Pohyb elektronu v elektrickém poli je jedním z nejdůležitějších fyzikálních procesů pro elektrotechniku. obrázek Podívejme se, jak se to děje ve vakuu. Uvažujme nejprve příklad pohybu elektronu od katody k anodě v rovnoměrném elektrickém poli.

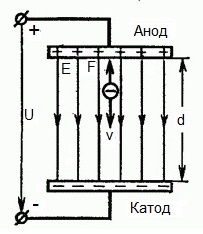
Obrázek níže ukazuje situaci, kdy elektron opouští zápornou elektrodu (katodu) se zanedbatelně malou počáteční rychlostí (sklonem k nule) a vstupuje v rovnoměrném elektrickém polipřítomen mezi dvěma elektrodami.

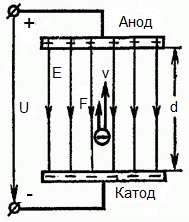
Na elektrody je přivedeno konstantní napětí U a elektrické pole má odpovídající sílu E. Vzdálenost mezi elektrodami je rovna d. V tomto případě bude na elektron působit ze strany pole síla F, která je úměrná náboji elektronu a síle pole:

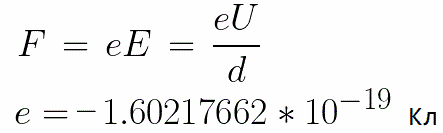
Protože elektron má záporný náboj, bude tato síla namířena proti vektoru intenzity pole E. V souladu s tím bude elektron urychlován v tomto směru elektrickým polem.

Zrychlení elektronu je úměrné velikosti síly F, která na něj působí, a nepřímo úměrné hmotnosti elektronu m.Protože je pole rovnoměrné, lze zrychlení pro daný obrázek vyjádřit jako:

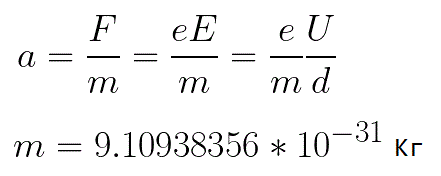
V tomto vzorci je poměr náboje elektronu k jeho hmotnosti specifický náboj elektronu, veličina, která je fyzikální konstantou:

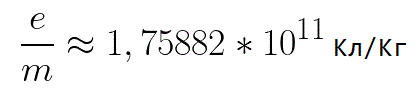
Elektron je tedy v urychlujícím elektrickém poli, protože směr počáteční rychlosti v0 se shoduje se směrem síly F na straně pole a elektron se proto pohybuje rovnoměrně. Pokud nejsou žádné překážky, urazí dráhu d mezi elektrodami a určitou rychlostí v dosáhne anodu (kladnou elektrodu). V okamžiku, kdy elektron dosáhne anody, bude jeho kinetická energie odpovídajícím způsobem rovna:

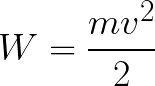
Protože po celé dráze d je elektron urychlován silami elektrického pole, získává tuto kinetickou energii jako výsledek práce síly působící na stranu pole. Tato práce se rovná:

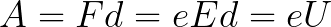
Potom lze kinetickou energii získanou elektronem pohybujícím se v poli zjistit takto:

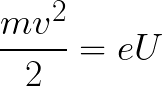
To znamená, že to není nic jiného než práce sil pole k urychlení elektronu mezi body s rozdílem potenciálu U.

V takových situacích je pro vyjádření energie elektronu vhodné použít takovou jednotku měření, jako je „elektronvolt“, který se rovná energii elektronu při napětí 1 voltu. A protože náboj elektronu je konstantní, pak 1 elektrovolt je také konstantní hodnota:

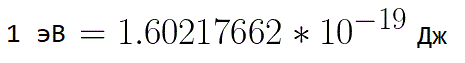
Z předchozího vzorce můžete snadno určit rychlost elektronu v kterémkoli bodě jeho dráhy při pohybu ve zrychlujícím se elektrickém poli, přičemž znáte pouze potenciální rozdíl, který prošel při zrychlení:

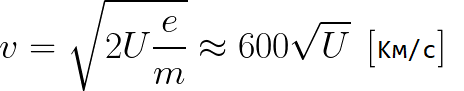
Jak vidíme, rychlost elektronu v urychlovacím poli závisí pouze na potenciálovém rozdílu U mezi koncovým bodem a počátečním bodem jeho dráhy.

Představte si, že se elektron začne vzdalovat od katody zanedbatelnou rychlostí a napětí mezi katodou a anodou je 400 voltů. V tomto případě bude v okamžiku dosažení anody její rychlost rovna:

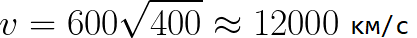
Je také snadné určit čas potřebný k tomu, aby elektron urazil vzdálenost d mezi elektrodami. Při rovnoměrně zrychleném pohybu z klidu se zjistí, že průměrná rychlost je polovina konečné rychlosti, pak se doba zrychleného letu v elektrickém poli bude rovnat:

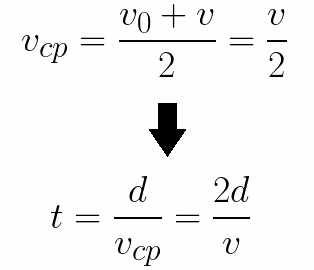
Podívejme se nyní na příklad, kdy se elektron pohybuje ve zpomalujícím se stejnoměrném elektrickém poli, to znamená, že pole směřuje jako dříve, ale elektron se začne pohybovat opačným směrem — od anody ke katodě.

Předpokládejme, že elektron opustil anodu s určitou počáteční rychlostí v a zpočátku se začal pohybovat ve směru katody. V tomto případě bude síla F působící na elektron ze strany elektrického pole namířena proti vektoru elektrické intenzity E — od katody k anodě.

Začne snižovat počáteční rychlost elektronu, to znamená, že pole elektron zpomalí. To znamená, že elektron se za těchto podmínek začne pohybovat rovnoměrně a rovnoměrně pomalu. Situace je popsána následovně: "elektron se pohybuje ve zpomalujícím elektrickém poli."

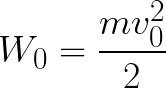
Od anody se elektron začal pohybovat s nenulovou kinetickou energií, která se při zpomalování začíná snižovat, protože energie je nyní vynaložena na překonání síly působící z pole na elektron.

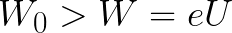
Pokud by počáteční kinetická energie elektronu při výstupu z anody byla okamžitě větší než energie, kterou musí pole vynaložit na urychlení pohybu elektronu od katody k anodě (jako v prvním příkladu), pak by elektron urazit vzdálenost d a nakonec se dostane ke katodě i přes brzdění.

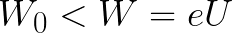
Pokud je počáteční kinetická energie elektronu menší než tato kritická hodnota, elektron ke katodě nedosáhne. V určitém bodě se zastaví a poté začne rovnoměrně zrychlený pohyb zpět k anodě. V důsledku toho mu pole vrátí energii, která byla vynaložena v procesu zastavení.

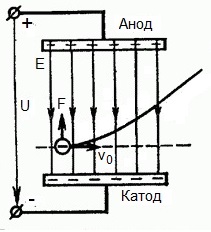
Co když ale elektron letí rychlostí v0 v oblasti působení elektrického pole v pravém úhlu? Je zřejmé, že síla na straně pole v této oblasti směřuje pro elektron od katody k anodě, tedy proti vektoru intenzity elektrického pole E.

To znamená, že nyní má elektron dvě složky pohybu: první – s rychlostí v0 kolmou k poli, druhá – rovnoměrně zrychlená působením síly ze strany pole směřující k anodě.

Ukazuje se, že po vlétnutí do akčního pole se elektron pohybuje po parabolické trajektorii. Ale po vylétnutí z oblasti působení pole bude elektron pokračovat ve svém rovnoměrném pohybu setrvačností po přímkové dráze.