Aktivní odpor a induktor ve střídavém obvodu

Uvažujme střídavý obvod obsahující pouze indukční odpor (viz článek "Induktor v obvodu střídavého proudu"), předpokládali jsme, že činný odpor tohoto obvodu je nulový.

Ve skutečnosti má jak vodič cívky samotné, tak propojovací vodiče malý, ale aktivní odpor, takže obvod nevyhnutelně spotřebovává energii zdroje proudu.

Při určování celkového odporu vnějšího obvodu je proto nutné sečíst jeho jalové a činné odpory. Je však nemožné sčítat tyto dva odpory, které jsou svou povahou odlišné.

V tomto případě se impedance obvodu ke střídavému proudu zjistí geometrickým sčítáním.

Sestrojí se pravoúhlý trojúhelník (viz obrázek 1), jehož jedna strana je hodnota indukčního odporu a druhá strana je hodnota aktivního odporu. Požadovaná impedance obvodu je určena třetí stranou trojúhelníku.

Obrázek 1. Stanovení impedance obvodu obsahujícího indukční a aktivní odpor

Impedance obvodu se označuje latinským písmenem Z a měří se v ohmech. Z konstrukce je vidět, že celkový odpor je vždy větší než indukční a činný odpor braný zvlášť.

Algebraický výraz pro celkový odpor obvodu je:

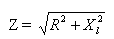
kde Z — celkový odpor, R — činný odpor, XL — indukční odpor obvodu.

Proto je celkový odpor obvodu proti střídavému proudu, který se skládá z aktivního a indukčního odporu, roven druhé odmocnině součtu druhých mocnin aktivního a indukčního odporu tohoto obvodu.

Ohmův zákon protože takový obvod je vyjádřen vzorcem I = U / Z, kde Z je celkový odpor obvodu.

Rozeberme si nyní, jaké bude napětí, pokud obvod má kromě a a fázového posunu mezi proudem a indukčností také relativně velký činný odpor. V praxi může být takovým obvodem např. obvod obsahující induktor se železným jádrem navinutým tenkým drátkem (vysokofrekvenční tlumivka).

V tomto případě již nebude fázový posun mezi proudem a napětím čtvrt periody (jako tomu bylo u obvodu s pouze indukčním odporem), ale mnohem menší; a čím větší odpor, tím menší fázový posun bude výsledkem.

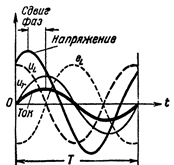
Obrázek 2. Proud a napětí v obvodu obsahujícím R a L.

Teď ona sama EMF samoindukce není v protifázi s aktuálním napětím zdroje, protože je posunuto vzhledem k napětí ne o polovinu periody, ale o méně.Navíc napětí vytvořené zdrojem proudu na svorkách cívky se nerovná emf vlastní indukce, ale je větší než je velikost úbytku napětí v aktivním odporu drátu cívky. Jinými slovy, napětí v cívce se tak jako tak skládá ze dvou složek:

• tiL- reaktivní složka napětí, která vyrovnává účinek EMF od samoindukce,

• tiR- aktivní složka napětí, která překoná aktivní odpor obvodu.

Pokud zapojíme velký aktivní odpor do série s cívkou, fázový posun se zmenší natolik, že aktuální sinusovka téměř dožene napěťovou sinusovku a rozdíl fází mezi nimi bude sotva patrný. amplituda členu a bude větší než amplituda členu.

Podobně můžete snížit fázový posun a dokonce jej úplně snížit na nulu, pokud nějakým způsobem snížíte frekvenci generátoru. Snížení frekvence bude mít za následek snížení samoindukčního EMF a tím i snížení fázového posunu mezi proudem a napětím v obvodu, který je jím způsoben.

Výkon střídavého obvodu obsahujícího induktor

Obvod střídavého proudu obsahující cívku nespotřebovává energii zdroje proudu a že v obvodu dochází k procesu výměny energie mezi generátorem a obvodem.

Pojďme nyní analyzovat, jak to bude s energií spotřebovanou takovým schématem.

Výkon spotřebovaný ve střídavém obvodu se rovná součinu proudu a napětí, ale protože proud a napětí jsou proměnné veličiny, bude se měnit i výkon.V tomto případě můžeme určit hodnotu výkonu pro každý časový okamžik, pokud vynásobíme hodnotu proudu hodnotou napětí odpovídající danému časovému okamžiku.

Abychom získali graf výkonu, musíme vynásobit hodnoty přímkových segmentů, které definují proud a napětí v různých časech. Taková konstrukce je znázorněna na Obr. 3, a. Čárkovaný průběh p nám ukazuje, jak se mění výkon ve střídavém obvodu obsahujícím pouze indukční odpor.

Při konstrukci této křivky bylo použito následující pravidlo algebraického násobení: Když se kladná hodnota vynásobí zápornou hodnotou, získá se záporná hodnota, a když se vynásobí dvě záporné nebo dvě kladné hodnoty, získá se kladná hodnota.

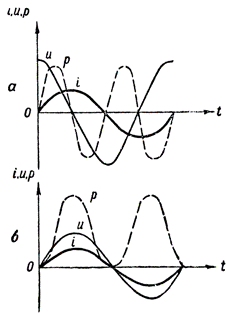
Obrázek 3. Výkonové grafy: a — v obvodu obsahujícím indukční odpor, b — také činný odpor

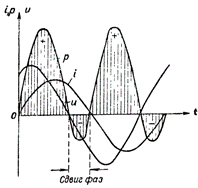
Obrázek 4. Graf výkonu pro obvod obsahující R a L.

Výkonová křivka v tomto případě leží nad časovou osou. To znamená, že nedochází k výměně energie mezi generátorem a obvodem, a proto je výkon dodávaný generátorem do obvodu zcela spotřebován obvodem.

Na Obr. 4 znázorňuje graf výkonu pro obvod obsahující jak indukční, tak aktivní odpor. V tomto případě dochází také ke zpětnému přenosu energie z obvodu do zdroje proudu, ale v mnohem menší míře než v obvodu s jediným indukčním odporem.

Po přezkoumání výše uvedených grafů výkonu jsme dospěli k závěru, že pouze fázový posun mezi proudem a napětím v obvodu vytváří "záporný" výkon.V tomto případě platí, že čím větší je fázový posun mezi proudem a napětím v obvodu, tím méně energie bude obvod spotřebovávat, a naopak, čím menší je fázový posun, tím větší výkon obvod spotřebuje.

Přečtěte si také: Co je napěťová rezonance