Trojúhelníky napětí, odporů a výkonů
Každý, kdo má představu o vektorových diagramech, si snadno všimne, že na nich lze velmi jasně rozlišit pravoúhlý napěťový trojúhelník, jehož každá strana odráží: celkové napětí obvodu, napětí aktivního odporu a napětí na reaktanci.
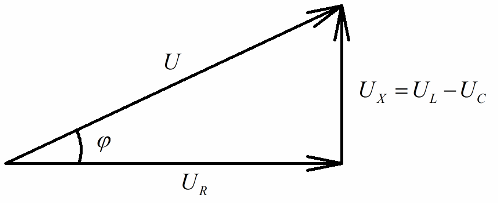
V souladu s Pythagorovou větou bude vztah mezi těmito napětími (mezi celkovým napětím obvodu a napětím jeho částí) vypadat takto:
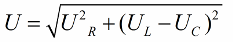
Pokud je dalším krokem vydělení hodnot těchto napětí proudem (proud protéká všemi sekcemi sériového obvodu stejně), pak Ohmův zákon dostaneme hodnoty odporu, to znamená, že nyní můžeme mluvit o pravoúhlém trojúhelníku odporů:
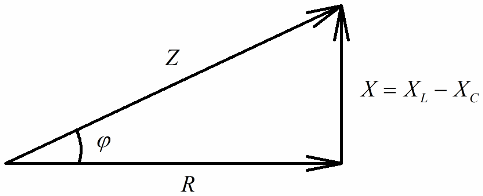
Obdobným způsobem (jako v případě napětí), pomocí Pythagorovy věty, lze stanovit vztah mezi impedancí obvodu a reaktancemi. Vztah bude vyjádřen následujícím vzorcem:
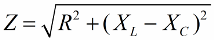
Poté vynásobíme hodnoty odporu proudem, ve skutečnosti zvýšíme každou stranu pravoúhlého trojúhelníku o určitý počet. Výsledkem je pravoúhlý trojúhelník s kapacitami:
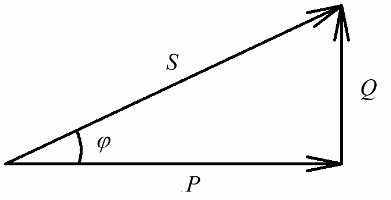
Činný výkon uvolněný při aktivním odporu obvodu spojený s nevratnou přeměnou elektrické energie (na teplo, při výkonu práce v instalaci) bude jednoznačně souviset s jalovým výkonem zapojeným do vratné přeměny energie (vytvoření magnetických a elektrických polí v cívkách a kondenzátorech) a s plným výkonem dodávaným do elektrické instalace.
Činný výkon se měří ve wattech (W), jalový výkon — ve varis (VAR — voltampérový reaktivní), celkový — ve VA (voltampér).
Podle Pythagorovy věty máme právo psát:
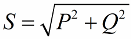
Věnujme nyní pozornost, že ve výkonovém trojúhelníku je úhel fí, jehož kosinus lze snadno určit především činným výkonem a zdánlivým výkonem. Kosinus tohoto úhlu (cos phi) nazývaný účiník. Ukazuje, kolik z celkového výkonu připadá na užitečnou práci v elektrické instalaci a není vráceno do sítě.
Je zřejmé, že vyšší účiník (maximální jeden) indikuje vyšší účinnost přeměny energie dodávané do zařízení pro provoz. Pokud je účiník 1, pak se veškerá dodaná energie spotřebuje na práci.
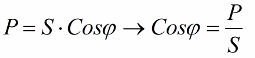
Získané poměry umožňují vyjádřit aktuální spotřebu instalace z hlediska účiníku, činného výkonu a síťového napětí:
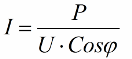
Čím je tedy kosinus phi menší, tím větší proud potřebuje síť k provedení určité práce. V praxi tento faktor (maximální síťový proud) omezuje přenosovou kapacitu přenosové linky, a proto čím nižší je účiník, tím větší je zatížení linky a tím menší je užitečná šířka pásma (nízký kosinus phi vede k omezení ). Ztráty joulů v elektrických vedeních s klesajícím kosinus phi lze vidět z následujícího vzorce:
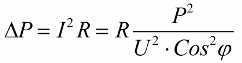
Na aktivním odporu R přenosového vedení se ztráty zvyšují tím více, čím vyšší je proud I, i když je reaktivní vůči zátěži. Můžeme tedy říci, že s nízkým účiníkem se náklady na přenos elektřiny jednoduše zvyšují. To znamená, že zvýšení kosinus phi je důležitým národohospodářským úkolem.
Je žádoucí, aby se jalová složka celkového výkonu blížila nule.K tomu by bylo dobré používat elektromotory a transformátory vždy při plné zátěži a po skončení používání je vypnout, aby nestály naprázdno. Naprázdno mají motory a transformátory velmi nízký účiník. Jedním ze způsobů, jak zvýšit kosinus phi u uživatelů, je použití kondenzátorové banky a synchronní kompenzátory.
