zdroj stejnosměrného proudu

Definice a vzorce

Výkon Je práce vykonaná za jednotku času. Elektrický výkon se rovná součinu proudu a napětí: P = U ∙ I. Další výkonové vzorce lze odvodit zde:

P = r ∙ I ∙ I = r ∙ I ^ 2;

P = U ∙ U / r = U ^ 2 / r.

Jednotku měření výkonu získáme nahrazením jednotek měření napětí a proudu ve vzorci:

[P] = 1 B ∙ 1 A = 1 BA.

Jednotka měření elektrického výkonu rovnající se 1 VA se nazývá watt (W). Název voltampér (VA) se používá v technice střídavého proudu, ale pouze pro měření zdánlivého a jalového výkonu.

Jednotky pro měření elektrického a mechanického výkonu jsou připojeny pomocí následujících připojení:

1 W = 1 / 9,81 kg • m / s ≈ 1 / 10 kg • m / s;

1 kg • m/s = 9,81 W ≈10 W;

1 hp = 75 kg • m/s = 736 W;

1 kW = 102 kg • m/s = 1,36 hp

Pokud nepočítáte s nevyhnutelnými energetickými ztrátami, motor o výkonu 1 kW dokáže každou sekundu přečerpat 102 litrů vody do výšky 1 m nebo 10,2 litru vody do výšky 10 m.

Elektrická energie se měří wattmetrem.

Příklady

1. Topné těleso elektrické pece o výkonu 500 W a napětí 220 V je vyrobeno z vysokoodporového drátu.Vypočítejte odpor prvku a proud, který jím protéká (obr. 1).

Proud najdeme vzorcem elektrického výkonu P = U ∙ I,

odkud I = P / U = (500 Bm) / (220 V) = 2,27 A.

Odpor se vypočítá podle jiného vzorce výkonu: P = U ^ 2 / r,

kde r = U^ 2 / P = (220 ^ 2) / 500 = 48400/500 = 96,8 Ohm.

Rýže. 1.

2. Jaký odpor by měla mít spirálka (obr. 2) na desce při proudu 3 A a výkonu 500 W?

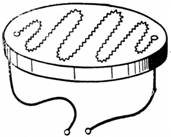
Rýže. 2.

Pro tento případ použijte jiný mocninný vzorec: P = U ∙ I = r ∙ I ∙ I = r ∙ I ^ 2;

proto r = P/I ^ 2 = 500/3 ^ 2 = 500/9 = 55,5 ohmů.

3. Jaký výkon se přemění na teplo s odporem r = 100 Ohm, které je připojeno do sítě o napětí U = 220 V (obr. 3)?

P = U^ 2/r = 220 ^ 2/100 = 48 400/100 = 484 W.

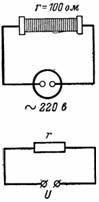
Rýže. 3.

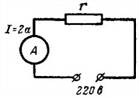
4. Ve schématu na Obr. 4 ampérmetr ukazuje proud I = 2 A. Vypočítejte odpor uživatele a spotřebovaný elektrický výkon v odporu r = 100 Ohm při připojení k síti s napětím U = 220 V.

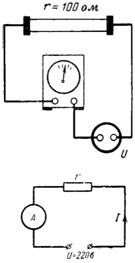
Rýže. 4.

r = U/I = 220/2 = 110 Ohm;

P = U ∙ I = 220 ∙ 2 = 440 W nebo P = U ^ 2/r = 220 ^ 2/110 = 48 400/110 = 440 W.

5. Lampa ukazuje pouze své jmenovité napětí 24 V. Pro určení zbývajících údajů lampy sestavíme obvod znázorněný na Obr. 5. Reostatem nastavte proud tak, aby voltmetr připojený na svorky svítilny ukazoval napětí Ul = 24 V. Ampérmetr ukazoval proud I = 1,46 A. Jaký výkon a odpor má svítilna a k jakým ztrátám napětí a výkonu dochází. u reostatu?

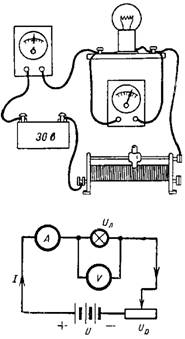
Rýže. 5.

Výkon lampy P = Ul ∙ I = 24 ∙ 1,46 = 35 W.

Jeho odpor je rl = Ul / I = 24 / 1,46 = 16,4 ohmů.

Pokles napětí reostatu Uр = U-Ul = 30-24 = 6 V.

Ztráta výkonu v reostatu Pр = Uр ∙ I = 6 ∙ 1,46 = 8,76 W.

6. Na štítku elektrické pece jsou uvedeny její jmenovité údaje (P = 10 kW; U = 220 V).

Určete, jaký odpor má pec a jaký proud jí prochází během provozu P = U ∙ I = U ^ 2 / r;

r = U^ 2/P = 220 ^ 2/10000 = 48400/10000 = 4,84 Ohmů; I = P/U = 10 000/220 = 45,45 A.

Rýže. 6.

7. Jaké je napětí U na svorkách generátoru, je-li při proudu 110 A jeho výkon 12 kW (obr. 7)?

Protože P = U ∙ I, pak U = P / I = 12 000/110 = 109 V.

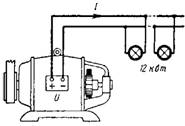
Rýže. 7.

8. Na schématu na Obr. 8 znázorňuje činnost elektromagnetické proudové ochrany. Při určitém proudu EM elektromagnet, držený pružinou P, přitáhne kotvu, otevře kontakt K a přeruší proudový obvod. V našem příkladu proudová ochrana přeruší proudový obvod při proudu I≥2 A. Kolik 25W žárovek lze rozsvítit současně při síťovém napětí U = 220 V, aby omezovač nefungoval?

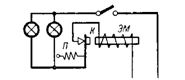
Rýže. osm.

Ochrana se spouští při I = 2 A, tzn. při výkonu P = U ∙ I = 220 ∙ 2 = 440 W.

Vydělením celkového výkonu jedné lampy dostaneme: 440/25 = 17,6.

Současně může svítit 17 lamp.

9. Elektrická trouba má tři topná tělesa o výkonu 500 W a napětí 220 V, zapojená paralelně.

Jaký je celkový odpor, proud a výkon při provozu trouby (obr. 91)?

Celkový výkon pece je P = 3 ∙ 500 W = 1,5 kW.

Výsledný proud je I = P / U = 1500/220 = 6,82 A.

Výsledný odpor r = U / I = 220 / 6,82 = 32,2 Ohm.

Proud jednoho článku je I1 = 500/220 = 2,27 A.

Odpor jednoho prvku: r1 = 220 / 2,27 = 96,9 Ohm.

Rýže. devět.

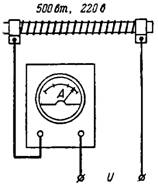
10. Vypočítejte odpor a proud uživatele, pokud wattmetr ukazuje výkon 75 W při síťovém napětí U = 220 V (obr. 10).

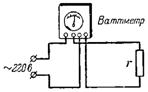
Rýže. deset.

Protože P = U ^ 2 / r, pak r = U ^ 2 / P = 48400/75 = 645,3 ohmů.

Proud I = P / U = 75/220 = 0,34 A.

11. Přehrada má pokles hladiny h = 4 m. Každou sekundu se do turbíny dostane potrubím 51 litrů vody. Jaký mechanický výkon se v generátoru přemění na elektrický výkon, pokud se neberou v úvahu ztráty (obr. 11)?

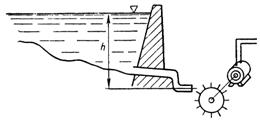
Rýže. jedenáct.

Mechanický výkon Pm = Q ∙ h = 51 kg / s ∙ 4 m = 204 kg • m / s.

Proto je elektrický výkon Pe = Pm: 102 = 204: 102 = 2 kW.

12. Jakou kapacitu musí mít motor čerpadla, aby každou sekundu přečerpal 25,5 litrů vody z hloubky 5 m do nádrže umístěné ve výšce 3 m? Ztráty se neberou v úvahu (obr. 12).

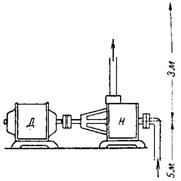
Rýže. 12.

Celková výška stoupání vody h = 5 + 3 = 8 m.

Mechanický výkon motoru Pm = Q ∙ h = 25,5 ∙ 8 = 204 kg • m / sec.

Elektrický výkon Pe = Pm: 102 = 204: 102 = 2 kW.

13. Vodní elektrárna přijímá z nádrže pro jednu turbínu každou sekundu 4 m3 vody. Rozdíl mezi hladinami vody v nádrži a turbíně je h = 20 m. Určete kapacitu jedné turbíny bez uvažování ztrát (obr. 13).

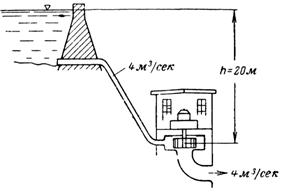
Rýže. 13.

Mechanický výkon proudící vody Pm = Q ∙ h = 4 ∙ 20 = 80 t/s • m; Pm = 80 000 kg • m/s.

Elektrický výkon jedné turbíny Pe = Pm: 102 = 80 000: 102 = 784 kW.

14. U paralelně buzeného stejnosměrného motoru jsou vinutí kotvy a budicí vinutí zapojeny paralelně. Vinutí kotvy má odpor r = 0,1 Ohm a proud kotvy I = 20 A. Budicí vinutí má odpor rv = 25 Ohm a budicí proud je Iw = 1,2 A. Jaký výkon se ztratí ve dvou vinutích motoru ( obr. 14)?

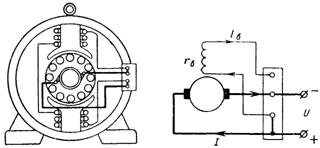
Rýže. čtrnáct.

Výkonové ztráty ve vinutí kotvy P = r ∙ I ^ 2 = 0,1 ∙ 20 ^ 2 = 40 W.

Výkonové ztráty budicí cívky

Pv = rv ∙ Iv ^ 2 = 25 ∙ 1,2 ^ 2 = 36 W.

Celkové ztráty ve vinutí motoru P + Pv = 40 + 36 = 76 W.

15. Varná deska na 220 V má čtyři přepínatelné stupně ohřevu, čehož je dosaženo rozdílovým zapínáním dvou topných těles s odpory r1 a r2, jak je znázorněno na obr. 15.

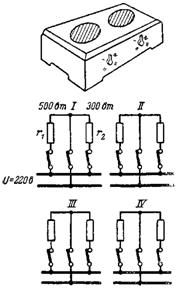
Rýže. 15.

Určete odpory r1 a r2, pokud má první topné těleso výkon 500 W a druhé 300 W.

Protože výkon uvolněný v odporu je vyjádřen vzorcem P = U ∙ I = U ^ 2 / r, odpor prvního topného článku

r1 = U ^ 2/P1 = 220 ^ 2/500 = 48 400/500 = 96,8 Ohm,

a druhý topný článek r2 = U^ 2/P2 = 220 ^ 2/300 = 48400/300 = 161,3 ohmů.

V poloze IV stupně jsou odpory zapojeny do série. Výkon elektrického sporáku v této poloze se rovná:

P3 = U^2/ (r1 + r2) = 220^2/ (96,8 + 161,3) = 48 400 / 258,1 = 187,5 W.

V poloze I. stupně jsou topná tělesa zapojena paralelně a výsledný odpor je: r = (r1 ∙ r2) / (r1 + r2) = (96,8 ∙ 161,3) / (96,8 + 161,3) = 60,4 Ohm.

Výkon dlaždic v pozici kroku I: P1 = U ^ 2 / r = 48 400 / 60,4 = 800 W.

Stejný výkon získáme sečtením výkonů jednotlivých topných těles.

16. Žárovka s wolframovým vláknem je určena pro výkon 40 W a napětí 220 V. Jaký odpor a proud má žárovka ve studeném stavu a při provozní teplotě 2500 °C?

Výkon lampy P = U ∙ I = U ^ 2 / r.

Proto je odpor vlákna žárovky v horkém stavu rt = U ^ 2 / P = 220 ^ 2/40 = 1210 Ohm.

Odolnost studeného závitu (při 20 °C) je určena vzorcem rt = r ∙ (1 + α ∙ ∆t),

odkud r = rt / (1 + α ∙ ∆t) = 1210 / (1 + 0,004 ∙ (2500-20)) = 1210 / 10,92 = 118 ohmů.

Proud I = P / U = 40/220 = 0,18 A prochází závitem lampy v horkém stavu.

Zapínací proud je: I = U / r = 220/118 = 1,86 A.

Po zapnutí je proud asi 10krát větší než proud horké lampy.

17. Jaké jsou ztráty napětí a výkonu v měděném vrchním vodiči elektrifikované dráhy (obr. 16)?

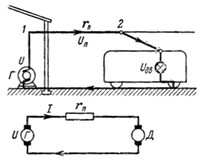
Rýže. 16.

Vodič má průřez 95 mm2. Motor elektrického vlaku odebírá proud 300 A ve vzdálenosti 1,5 km od zdroje energie.

Ztráta (pokles) napětí ve vedení mezi body 1 a 2 Up = I ∙ rπ.

Odpor trolejového drátu rp = (ρ ∙ l) / S = 0,0178 ∙ 1500/95 = 0,281 Ohm.

Pokles napětí v trolejovém drátu Up = 300 ∙ 0,281 = 84,3 V.

Napětí Ud na svorkách D motoru bude o 84,3 V menší než napětí U na svorkách G zdroje.

Úbytek napětí v troleji při pohybu elektrického vlaku se mění. Čím více se elektrický vlak vzdaluje od zdroje proudu, tím je vedení delší, což znamená větší jeho odpor a úbytek napětí na něm.Proud na kolejích se vrací do uzemněného zdroje G. Odpor kolejí a země je prakticky nulová.