Logická zařízení

Logická algebra nebo Booleova algebra se používá k popisu zákonů činnosti číslicových obvodů. Algebra logiky je založena na konceptu „události“, která se může nebo nemusí stát. Událost, která nastala, je považována za pravdivou a je vyjádřena logická úroveň «1», událost, která nenastala, je považována za nepravdivou a je vyjádřena logická úroveň «0».

Událost je ovlivněna proměnnými a ty ovlivňují podle určitého zákona. Tento zákon se nazývá logická funkce, proměnné jsou argumenty... Che. logickou funkcí je funkce y = f (x1, x2, … xn), která nabývá hodnot «0» nebo «1». Proměnné x1, x2, … xn mají také hodnoty «0» nebo «1».

Algebra logiky — odvětví matematické logiky, které studuje strukturu složitých logických tvrzení a způsoby, jak stanovit jejich pravdivost algebraickými metodami. Ve vzorcích logické algebry jsou proměnné logické nebo binární, to znamená, že nabývají pouze dvou hodnot - nepravda a pravda, které jsou označeny 0 a 1. Každý počítačový program obsahuje logické operace.

Zařízení určená k vytváření funkcí logické algebry se nazývají logická zařízení... Logické zařízení má libovolný počet vstupů a pouze jeden výstup (obr. 1).

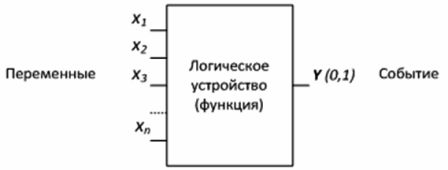
Obrázek 1 — Logické zařízení

Například elektronický kombinační zámek obsahuje logické zařízení, pro které událostí (y) je otevření zámku. Aby událost (y = 1) nastala, tzn. zámek se otevřel, je nutné definovat proměnné — deset tlačítek na numerické klávesnici. Některá tlačítka musí být stisknuta, tzn. vezměte hodnotu «1» a současně stiskněte v určitém pořadí — logická funkce.

Libovolnou logickou funkci je vhodné reprezentovat formou stavové tabulky (pravdivé tabulky), kde jsou zaznamenány možné kombinace proměnných (argumentů) a odpovídající hodnota funkce.

Logická zařízení jsou postavena na logických hradlech, které plní specifickou funkci. Základní logické funkce jsou logické sčítání, logické násobení a logická negace.

1) OR (OR) — logické sčítání nebo dělení (z angl. disjunkce — přerušení) — logická jednotka se objeví na výstupu tohoto prvku, když se jednotka objeví alespoň na jednom ze vstupů. Výstup bude logická nula pouze tehdy, když je na všech vstupech signál logické nuly.

Tuto operaci lze provést pomocí kontaktního obvodu se dvěma paralelně zapojenými kontakty. «1» na výstupu takového obvodu se objeví, pokud je alespoň jeden z kontaktů sepnutý.

2) AND (AND) — logické násobení nebo spojení (z anglického union — connection, & — ampersand) — na výstupu tohoto prvku se signál logické jednotky objeví pouze tehdy, když je logická jednotka přítomna na všech vstupech.Pokud je alespoň jeden vstup nulový, bude nula i výstup.

Tato operace může být provedena kontaktním obvodem sestávajícím z kontaktů zapojených do série.

3) NOT — logická negace nebo inverze označená pomlčkou nad proměnnou — operace se provádí na jedné proměnné x a hodnota y je opačná k této proměnné.

Operaci NELZE provést pomocí normálně sepnutého kontaktu elektromagnetického relé: na cívce relé není žádné napětí (x = 0) — kontakt je sepnut i na výstupu «1» (y = 1). Při přítomnosti napětí na cívce relé (x = 1) je kontakt rozpojen i na výstupu «0» (y = 0).

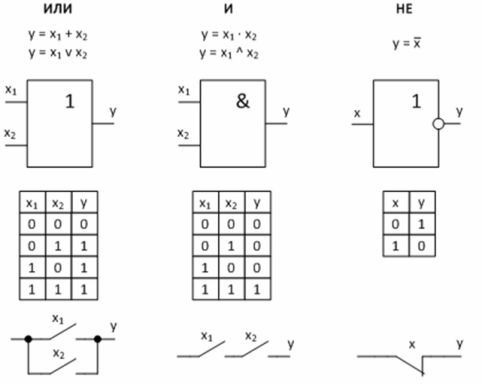
Obrázek 2 — Základní logické funkce a jejich implementace

Logická zařízení používají různá logická hradla. Zvláště důležité jsou dvě univerzální logické operace, z nichž každá je schopna nezávisle tvořit libovolnou logickou funkci.

4) NAND — Schaeferova funkce.

5) OR NOT — Funkce děrování.

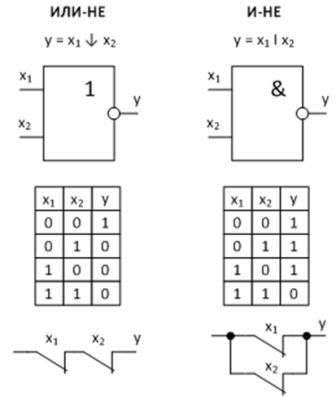
Obrázek 3 — Univerzální logické funkce a jejich implementace

Příklad: Bezpečnostní poplachový obvod založený na logických prvcích. Generátor G generuje signál sirény a přivádí jej do zesilovacího stupně přes logický prvek «AND» mikroobvodu DD2. Při sepnutých ochranných spínačích S1 — S4 působí na vstupy prvku DD1 úroveň «0» — úroveň «0» je na spodním vstupu prvku «I» DD2, což znamená, že hradlo tranzistoru VT je také „0“.

V případě rozpojení alespoň jednoho ze spínačů, například S1, bude vstup prvku DD1 přes odpor R1 přijímat napětí úrovně «1», což způsobí výskyt «1» na druhém vstupu prvek «AND» DD1.To umožní, aby signál z generátoru G prošel do brány tranzistoru, jehož zátěží je reproduktor.

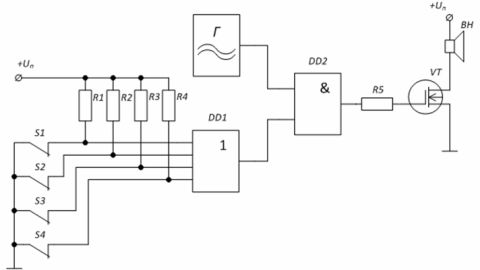
Obrázek 4 – Schéma ochrany poplachu

Složité digitální obvody jsou stavěny opakováním základních logických obvodů znovu a znovu. Nástrojem pro takovou konstrukci je Booleova algebra, která se z hlediska digitální technologie nazývá logická algebra. Na rozdíl od proměnné v běžné algebře má booleovská proměnná pouze dvě hodnoty, které se nazývají booleovská nula a booleovská jedna.

Logická nula a logická jednička se značí 0 a 1. V logické algebře nejsou 0 a 1 čísla, ale logické proměnné. V logické algebře existují tři základní operace mezi logickými proměnnými: logické násobení (konjunkce), logické sčítání (disjunkce) a logická negace (inverze).

Elektronické obvody plnící stejnou logickou funkci, ale sestavené z různých prvků, lišících se spotřebou energie, napájecím napětím, hodnotami vysokého a nízkého výstupního napětí, dobou zpoždění šíření signálu a nosností.

Viz také k tomuto tématu: Logická hradla AND, OR, NOT, AND-NOT, OR-NOT a jejich pravdivostní tabulky